Undergraduate Convexity

From Fourier and Motzkin to Kuhn and Tucker

Niels Lauritzen

• Publisher: WSPC
• Year: 2013
• Print ISBN:
  9789814452762
• eBook ISBN:
  9789814412537
• Topic: Matemáticas
• Subtopic: Matemática aplicada

Based on undergraduate teaching to students in computer science, economics and mathematics at Aarhus University, this is an elementary introduction to convex sets and convex functions with emphasis on concrete computations and examples.

Starting from linear inequalities and Fourier–Motzkin elimination, the theory is developed by introducing polyhedra, the double description method and the simplex algorithm, closed convex subsets, convex functions of one and several variables ending with a chapter on convex optimization with the Karush–Kuhn–Tucker conditions, duality and an interior point algorithm.

Contents:

• Fourier–Motzkin Elimination
• Affine Subspaces
• Convex Subsets
• Polyhedra
• Computations with Polyhedra
• Closed Convex Subsets and Separating Hyperplanes
• Convex Functions
• Differentiable Functions of Several Variables
• Convex Functions of Several Variables
• Convex Optimization
• Appendices:
  • Analysis
  • Linear (In)dependence and the Rank of a Matrix

Readership: Undergraduates focusing on convexity and optimization.

Chapter 1

Fourier-Motzkin elimination

You probably agree that it is easy to solve the equation

This is an example of a linear equation in one variable having the unique solution x = 2. Perhaps you will be surprised to learn, that there is essentially no difference between solving a simple equation like (1.1) and the more complicated system

of linear equations in x, y and z. Using the first equation 2x + y + z = 7 we solve for x and get

This may be substituted into the remaining two equations in (1.2) and we get the simpler system

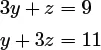
of linear equations in y and z. Again using the first equation in this system we get

ending up with the simple equation 8z = 24. This is an equation of the type in (1.1) giving z = 3. Now z = 3 gives y = 2 using (1.4). Finally y = 2 and z = 3 gives x = 1 using (1.3).

Figure 1.1: Isaac Newton (1642–1727). English mathematician.

Solving a seemingly complicated system of linear equations like (1.2) is really no more difficult than solving the simple equation (1.1). One of the world's greatest scientists, Isaac Newton, found it worthwhile to record this method in 1720 with the words

And you are to know, that by each Æquation one unknown Quantity may be taken away, and consequently, when there are as many Æquations and unknown Quantities, all at length may be reduc'd into one, in which there shall be only one Quantity unknown.

Figure 1.2: Carl Friedrich Gauss (1777–1855). German mathematician.

During the computation of the orbit of the asteroid Pallas around 1810, Gauss encountered the need for solving linear equations related to his famous least squares method. If you spend a little time deciphering the Latin in Gauss's original writings (see Figure 1.3), you will see how elimination appears naturally towards the end of the page. In spite of Newton's explicit ...

Table of contents

• Cover
• Title Page
• Copyright
• Preface
• Acknowledgments
• 1. Fourier-Motzkin elimination
• 2. Affine subspaces
• 3. Convex subsets
• 4. Polyhedra
• 5. Computations with polyhedra
• 6. Closed convex subsets and separating hyperplanes
• 7. Convex functions
• 8. Differentiable functions of several variables
• 9. Convex functions of several variables
• 10. Convex optimization
• Appendix A Analysis
• Appendix B Linear (in) dependence and the rank of a matrix
• Bibliography
• Index