Geometry Of The Octonions, The

Tevian Dray, Corinne A Manogue

• Publisher: World Scientific Publishing Company
• eBook ISBN: 9789814401838
• Topic: Matematica
• Subtopic: Algebra astratta

There are precisely two further generalizations of the real and complex numbers, namely, the quaternions and the octonions. The quaternions naturally describe rotations in three dimensions. In fact, all (continuous) symmetry groups are based on one of these four number systems. This book provides an elementary introduction to the properties of the octonions, with emphasis on their geometric structure. Elementary applications covered include the rotation groups and their spacetime generalization, the Lorentz group, as well as the eigenvalue problem for Hermitian matrices. In addition, more sophisticated applications include the exceptional Lie groups, octonionic projective spaces, and applications to particle physics including the remarkable fact that classical supersymmetry only exists in particular spacetime dimensions.

Contents:

• • Introduction
• Number Systems:
  • The Geometry of the Complex Numbers
  • The Geometry of the Quaternions
  • The Geometry of the Octonions
  • Other Number Systems
• Symmetry Groups:
  • Some Orthogonal Groups
  • Some Unitary Groups
  • Some Symplectic Groups
  • Symmetry Groups over Other Division Algebras
  • Lie Groups and Lie Algebras
  • The Exceptional Groups
• Applications:
  • Division Algebras in Mathematics
  • Octonionic Eigenvalue Problems
  • The Physics of the Octonions
  • Magic Squares

Readership: Advanced undergraduate and graduate students and faculty in mathematics and physics; non-experts with moderately sophisticated mathematics background.
Key Features:

• This book is easily digestible by a large audience wanting to know the elementary introduction to octanions
• Suitable for any reader with a grasp of the complex numbers, although familiarity with non-octonionic versions of some of the other topics would be helpful
• Many open problems are very accessible
• Advanced topics covered are quite sophisticated, leading up to a clear discussion of (one representation of) the exceptional Lie algebras and their associated root diagrams, and of the octonionic projective spaces on which they act

Chapter 1

Introduction

What number systems allow the arithmetic operations of addition, subtraction, multiplication, and division?

In order to count, we need integers. How high can we count? There are finite number systems—and the universe itself may be finite—but let’s assume that we can count to infinity, or, more precisely, that there’s no largest number. In order to subtract, we also need zero, as well as negative numbers. As we said, we need the integers, namely

Integer arithmetic works fine for addition, subtraction, and multiplication, but what about division? Now we need fractions, or, more formally, the rational numbers

Now we can indeed do arithmetic. However, we cannot measure the hypotenuse of a right triangle, or the circumference of a circle. For those operations, we need the real numbers, denoted

, which include rational numbers such as 3 or

, but also irrational numbers such as

or π.

Are we done yet? No, because there are algebraic equations we still can’t solve. The simplest example is

whose solutions, if any, would be square roots of −1. As you may know, the complex numbers ℂ consist of both real numbers and real multiples of

. Furthermore, all nth order polynomial equations have exactly n solutions over ℂ (counting multiplicity). The complex numbers may seem like a mathematical toy; who needs the square root of negative numbers? It turns out that quantum mechanics is an inherently complex theory; complex numbers are an essential ingredient in our current understanding of the world around us.

Are we done yet? Maybe. What are the rules? Even over the complex numbers, the rules are slightly different, as evidenced by the apparent paradox

which forces us to rethink the rules for manipulating square roots. Can we change the rules in other ways?

Yes, we can. First of all, we can drop the requirement that numbers commute with each other. However counterintuitive this may feel, there is good reason to suspect that such numbers could be useful, since there are many physical operations where the order matters. A mathematical example where order matters is matrix multiplication, where in general AB ≠ BA. As we will see, this choice leads to the quaternions, ℍ.

Can we go further? Yes, by dropping associativity. Why would we do that? Well, matrix multiplication is associative, but the cross product is not. Can you work out

Not without knowing which product to do first! As we will see, this choice leads to the octonions,

.

Can we go further? No; going further requires us to give up division. More precisely, the four algebras ℝ, ℂ, ℍ, and

are the only ones without zero divisors, that is, nonzero elements whose product is nonetheless zero.

The octonions are thus nature’s largest division algebra. This author believes that this largest mathematical structure will ultimately be seen as the key to understanding the basic building blocks of nature, namely the fundamental particles such as electrons and quarks.

The goal of this book is to introduce the reader to the mathematics of the octonions, while offering some hints as to how they might be useful in physics. Let’s begin.

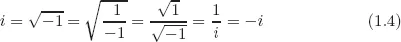
PART I

Number Systems

Chapter 2

The Geometry of the Complex Numbers

2.1Complex Numbers

Begin with the real numbers,

. Add “the” square root of −1; call it i. You have just constructed the complex numbers, ℂ, in the form

That is, a complex number z is a pair of real numbers(a, b), which is usually written as

and which can be thought of as either a point in the (complex) plane with coordinates (a, b) or as a vector with components a and b.

2.2History

Complex numbers were first used in the 16th century in order to solve cubic equations, as there are some cases with real solutions that nonetheless require the use of complex numbers in order to obtain those solutions. The recognition of the complex numbers as an object worthy of study in their own right is usually attributed to Rafael Bombelli, who in 1572 was the first to formalize the rules of complex arithmetic (and also, at the same time, the first to wri...

Table of contents

• Cover Page
• Title Page
• Copyright
• Preface
• Acknowledgments
• Contents
• List of Figures
• List of Tables
• 1. Introduction
• I. Number Systems
• II. Symmetry Groups
• III. Applications
• Further Reading
• Bibliography
• Index