Children′s Mathematics

Making Marks, Making Meaning

Elizabeth Carruthers, Maulfry Worthington

• Publisher: SAGE Publications Ltd
• Year: 2006
• Print ISBN: 9781412922838, 9781412922821
• eBook ISBN: 9781446224373
• Edition: 2
• Topic: Éducation
• Subtopic: Enseignement des mathématiques

?In Case Study 5 (a grassroots ?Children?s Mathematics Network group?) the initiative supported the participants in their professional change by giving them a space for the detailed and joint consideration of children?s mathematical thinking. Another significant feature of this initiative is its focus on careful consideration and analysis of children?s mathematics, and the ways in which professionals can support and encourage the children?s mathematical thinking and reasoning… The standard of the mathematical understanding, thinking and reasoning that the displays revealed was far higher than the specified curriculum objectives for children of this age…? - Researching Effective CPD in Mathematics Education (RECME) project: (NCETM, 2009)

?The review also plays great score by play-based learning of a mathematical nature, and makes specific recommendations regarding early mark-making as a precursor to abstract mathematical symbolism?. Section 115 features children?s mathematical graphics and emphasises: ?The role of mark-making in children?s cognitive development is set out in the taxonomy (Carruthers and Worthington, 2006)?. The report recommends that ?local authorities, leaders, managers and head teachers should provide a culture with a significant focus on mathematical mark-making? and ?a learning environment that encourages children to choose to use their own mathematical graphics to support their mathematical thinking and processes? - The Williams Maths Review: (DCSF, 2008)

`At the very heart of the success of the book is the authors? ability to see mathematics through young children?s eyes by listening to and reflecting on the constant efforts made by children to make sense of their world. This is a liberating book which proposes that the teaching of mathematics could and should be a highly creative and enjoyable proceess? - Branwen Llewelyn Jones, Early Years Consultant at PACE Ltd / TACTYC

?Ground breaking... To single out any one chapter would be unfair because there is something thought-provoking and inspirational throughout. If you want to expand your understanding upwards and outwards then get a copy soon? - Times Educational Supplement

?I first read Children?s Mathematics, Making Marks, Making Meaning a couple of years ago and it had an immediate impact on my own thinking and teaching, and the work I do with trainee teachers. I?m sure you will find it compelling reading too. I think it has the potential to change, in a fundamental way, how we think about early mathematical development? - Lynne McClure, Editor, Math Co-ordiator?s File, Mathematics Association

?In their exceptionally readable and informative book, Children?s Mathematics, Making Marks, Making Meaning Carruthers and Worthington (2006) draw attention to one of the main goals of early years teaching, that is, to help children make links between the mathematics they have already encountered (and continue to engage with) at home and the more abstract mathematics of the school. These authors suggest that by encouraging children to represent mathematical ideas in their own ways and, crucially, by talking to the pupils about the marks they have made, we are given a "window" onto their thinking that may otherwise be inaccessible? - Liz Pumphrey, NRICH

This book draws on the authors? many years of teaching children aged three to eight years and also on their extensive research with children in the home, nursery and school. The authors explain the development and range of young children?s mathematical marks and visual representations, showing how children make mental connections between their own early marks and subsequent abstract mathematical symbolism, and go on to develop their own written methods.

Combining theory and practice, this acclaimed book demonstrates how children?s own mathematical graphics are highly creative and show deep levels of thinking. The authors show how this is the key to success in school mathematics and to higher levels of achievement.

The authors are winners of TACTYC?s (2003) Jenefer Joseph Award for the Creative Arts (3 - 8) - awarded for their innovative work with children on mathematical graphics.

1	Who Takes Notice of Children’s Own ‘Written’ Mathematics?

In Antoine de Saint-Exupéry’s poignant tale he writes:

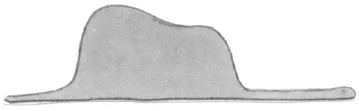
Once when I was six years old I saw a magnificent picture in a book, called True Stories from Nature, about the primeval forest. It was a picture of a boa constrictor in the act of swallowing an animal … I pondered deeply, then, over the adventures of the jungle. And after some work with a coloured pencil I succeeded in making my first drawing. My Drawing Number One. It looked like this:

Figure 1.1 Drawing Number One

I showed my masterpiece to the grown-ups, and asked them whether the drawing frightened them. But they answered: ‘Frighten? Why should any one be frightened by a hat?’
My drawing was not a picture of a hat. It was a picture of a boa constrictor digesting an elephant. But since the grown-ups were not able to understand it, I made another drawing: I drew the inside of the boa constrictor, so that the grown-ups could see it clearly.

Elles ont toujours besoin d’explications.

They always needed to have things explained …
I had been disheartened by the failure of my Drawing Number One and my Drawing Number Two. Grown-ups never understand anything by themselves, and it is tiresome for children to be always and forever explaining things to them (Saint-Exupéry, 1958, pp. 5–6).

In the spirit of Antoine de Saint-Exupéry’s internationally known and deeply moving fable, we have written this book to help ‘the grown-ups’ understand the meanings of young children’s mathematical images.

Children’s mathematical graphics

This book is a study of young children’s own mathematical graphics and the way in which they can use their own marks to make their own meanings. This allows children to more readily translate between their informal ‘home mathematics’ and the abstract symbolism of ‘school mathematics’: we argue that childrens’s own mathematical graphics (‘thinking on paper’) enables children to become bi-numerate.

Why write about children’s mathematical graphics?

For the past fifteen years we have developed our practice and explored the theories that underpin this book. Because we were teaching for a greater part of this period we were able to trial ideas, hypothesise and generate our philosophies and develop our pedagogy in our own settings. As our excitement in the development of children’s own mathematical marks and their meanings grew, we focused on a number of research projects that have helped inform and guide us. Where they have relevance for the subject of this book, we refer to our findings (see Appendix for a list of our research topics).

On numerous occasions we have been invited to share our practice, understanding and some of the hundreds of children’s examples we have collected – with students where we have lectured and with teachers on professional development courses and at Early Years conferences. Students’ and teachers’ responses are almost always of surprise and great interest – that it makes sense to encourage this, that working in this way offers a real alternative to the use of worksheets and, above all, that it offers tremendous insight into children’s understanding and development. But the benefits are greatest for the children.

We had come to children’s early mathematical mark-making through our own interest and following many years of experience in supporting emergent writing in our classrooms. We had seen wonderful progress in children’s early writing and began to make comparisons with children’s early recorded mathematics. A significant element in our development as teachers was the period in which we were members of the ‘Emergent Mathematics Teachers’ group’ (see this chapter).

As we developed our practice and theory we collected samples of children’s mathematical marks. For a greater part of this period we taught mainly in nursery and First Schools, and also through the primary age range to 11 years. Although we concentrate on the 3–8 age range in this book we feel the development of children’s own mathematics through the school is important.

It took time to develop our practice in order to support children’s mathematical graphics. Working with local groups of teachers encouraged us to question assumptions and consider different perspectives on teaching mathematics in the Early Years. As we slowly developed our practice we also traced the pattern of children’s early development of numerals and established some pathways that led to early calculations on paper. This development did not reveal itself to us as readily as children’s early writing had done.

Evidence-based study

The examples of children’s mathematics have come from our own teaching either in our own classrooms or when we were invited to teach in other classrooms. It is this strong teaching background, coupled with our work as consultants, advisers and lecturers, that has made us focus on what we believe is important in the Early Years. It has also sharpened our knowledge of underpinning theories – of mathematics and mark-making and of all the complexity of teaching and learning in the 3–8 years age range.

International findings

Our search for literature on children’s own written mathematics in the 3–8 age range did not reap any major findings. There were individual studies in the USA, for example Whitin, Mills and O’Keefe, (1990); in Australia, Stoessinger and Edmunds (1992) and in England teachers’ stories of their work (Atkinson, 1992). There was the beginning of a movement in the direction of advocating what we term a bi-numerate approach to the teaching of mathematics (see Chapter 5).

However, Alexander’s significant study of five nations – France, Russia, India, the USA and England – found that the teaching of mathematics worldwide is heavily influenced by textbooks and worksheets. India was the exception, not only because of funding difficulties, but due to significant historical and cultural factors (Alexander, 2000). In 1998 and again in 1999 I was fortunate to have two periods of voluntary work with a children’s charity in Tamil Nadu, in southern India. At first hand I was able to see children taught in nursery and primary schools.

State-run nursery schools are found in many larger villages, including those in which I worked. The nursery teacher may have completed primary education, though her assistants have often had little or no schooling, and in this rural area there was very little training for nursery teachers. In many of the villages I visited there were few literate adults and this, combined with often extreme levels of poverty, means that perhaps only a handful of homes in the community had any printed matter, pens or paper in their homes. Of the ten nursery schools I visited, nine were totally empty rooms: apart from the adults and children, there were no toys, resources, books or pictures. Discipline was strict with commands to ‘sit up straight’, ‘fold your arms’ and ‘sit still and be quiet’ frequent. The children attend nursery school until they are 6 years old.

In only one of the nursery schools I visited were there any visual aids. The teacher proudly showed me some small posters she had made – an alphabet with pictures and a small number frieze of numbers 1–10 with pictures. Questions were fired at these 2–6-year-olds and a rapid response was demanded. The mathematics teaching was a transmission model with an emphasis on correct answers. In the nursery schools I visited there were no opportunities for mark-making or drawing since there were no resources. During a period of several months I did not once see a child make marks on the sandy ground outside, even in play.

Teaching in primary schools was of a very similar style, although funding permitted children in some classes to use slates and older children to use exercise books. They copied standard algorithms from the blackboard and filled in the answers. Alexander includes a transcription of one spelling lesson (in a Hindi-speaking area) with children aged 5–6 years: this is typical of what I saw in every nursery and primary school I visited:

four children come to the blackboard at the teacher’s invitation, to write ‘A’. Teacher then writes ‘A’ herself and asks the class to recite the sound, over and over again. Teacher writes, ana, Anamika, aachi (pomegranate; a girl’s name; good) on the board. Three pupils come forward to circle the ‘A’ in these words. Class applauds. Teacher asks questions to recapitulate and children chant in response. (Alexander, 2000, p. 282)

Alexander reported that lessons he had observed in England in 1998 were as tied to textbooks and published schemes as those in Russian schools. Teachers in France and the USA were moving away from the domain of textbooks. Alexander emphasised the tension in the USA between those schools wanting to move away from the dominance of standard textbooks, and the concern of school boards and government to raise standards. The change noted was that instead of using workbooks exclusively, teachers created their own worksheets for children to record their mathematics set by the teacher. This finding is mirrored by our study (see Chapter 5).

Mathematics education in the Netherlands

In the Netherlands the main influence in mathematics education has been ‘Realistic Mathematics Education’ (REM). This was initiated by Freudenthal who professed that mathematics must be connected to society and children should learn mathematics by a process of ‘progressive mathematization’ (Freudenthal, 1968). Treffers built on this idea and describes two types of processes, horizontal and vertical (Treffers, 1978). ‘Horizontal mathematization’ is Freudenthal’s term to explain the way in which the gap between informal mathematics and formal mathematics is bridged. Horizontal mathematization helps children move from the world of real life into the world of symbols. In teaching terms, for example, a picture of a real-life problem is given to the children, perhaps people getting on and off a bus. This would later be shown with symbols and then again, after a period of time, shown without any picture cues (Heuvel-Panhuizen, 2001). The term ‘vertical mathematization’ refers to the children working within the world of symbols. Children move on to models such as the empty number line which the National Numeracy Strategy in England has adopted (QCA, 1999).

Mental arithmetic is at the ‘heart of the curriculum’ in schools in the Netherlands that use the REM curriculum (now the majority), (Buys, 2001). Children try to do every calculation mentally and are also encouraged to write their thinking down on scrap paper so that they remember the steps for more difficult calculations where it is impossible sometimes, to keep track. Children’s own ways of thinking are encouraged through their mental work, and informal recordings through the empty number line have a high priority.

Studies of Brazilian street children’s informal calculations have highlighted the significance of meaningful contexts for mathematics and emphasize the need to preserve meaning within classroom contexts. Nunes et al. propose that the Dutch Realistic Mathematics Education, in which problem solving is central, goes a long way in doing this (Nunes et al., 1993).

Whilst children in the Netherlands do not begin school until six years of age, in England most children now start school during their fourth year and it is largely for this reason that we have focused on children’s earliest marks and their development. Such a socio-cultural approach as REM, ‘integrates both the child’s personal constructions and the educator’s pedagogical responsibilities’ (Oers, 2004a, p. 71). The term ‘realistic’ in the Dutch curriculum refers not only to ‘connections to the real world …’ (but also) offering students ‘problem situations that they can imagine’ (Heuvel-Panhuizen, in Anghileri, 2001b, p. 51). Pupils following the REM curriculum ‘are expected … to develop models and to be able to proceed from their “own informal mathematical constructions to what could be accepted as formal mathematics”’ (Streefland, 1990, p. 1, in Nunes et al., 1993), something which we also expect children to do. Essentially the curriculum view is that ‘mathematics is a cultural activity that should not be reduced to correctly performing mathematical operations’ (Oers, 2002, p. 23).

A recent study (Anghileri, 2002a) compared pupils written calculations strategies in England with those of children in the Netherlands using the REM approach. The research emphasises that flexible calculation strategies are ‘more important than the use of one sophisticated strategy’ (Anghileri, 2002a, p. 1). Acknowledging this research, MEI argues that that in the Dutch approach ‘there is a much stronger sense that mastery develops over time, and that fluency has to go hand in hand with understanding (MEI, 2005, p. 73).

Whilst the majority of Dutch schools use the REM curriculum, work in the Netherlands based on a Vygotskian perspective has led to the Developmental Education curriculum (adopted by an increasing number of schools and preschools), with children of four to seven years of age, and this is supported by the Free University in Amsterdam. The Developmental Education approach supports children’s meaning-making through a play-based curriculum. Oers emphasises that whilst Vygotsky’s cultural-historical perspective (on which the core of the socio-cultural approach is based) is ‘still strongly activity based … the focus on meaning has become more explicit’ (Oers, 2004b, p. 1, 3). Interest in the cultural historical approach has grown internationally through the work of researchers including Jerome Bruner, Michael Cole, Barbara Valsiner and James Wertsch, (Oers, 2004b, p. 2) and has also been linked with the work of Bakhtin, Wells, Halliday and Dewey (Oers, 2004c, p. 1) and with Lave and Wenger’s situated learning (1991). Thus in the Netherlands, both the REM and the Developmental Curriculum appear to emphasise the importance of allowing pupils to attach personal meaning to the cultural transmission of mathematics.

Zevenbergen raises concerns about the philosophy that underpins mathematics curricula in Australia and many other western countries. Comparing the Dutch approach to that of Queensland in Australia, she argues that ‘while there are tokenistic references made to children’s informal understandings, these are not central to curriculum design’ (Zevenbergen, 2002, p. 4).

In 1999, England introduced the National Numeracy Strategy which is a framework of objectives for teaching mathematics for 5–11-year-olds (QCA, 1999). Like the Dutch model, this document also has a heavy emphasis on mental calculation but introduces standard and expanded written forms of mathematics much earlier. England, unlike other countries we have mentioned, has recognised the importance of young children’s own mathematical marks and their own choice of written methods have been highlighted in official documentation. Guidance for teachers emphasises: ‘children wil...

Table of contents

• Cover Page
• Title
• Copyright
• Contents
• About the Authors
• Acknowledgements
• Foreword by John Matthews
• Foreword by Chris Athey
• Preface
• 1 Who takes notice of children’s own ‘written’ mathematics?
• 2 Making marks, making meaning
• 3 Mathematical schemas
• 4 Early writing, early mathematics
• 5 Bridging the gap between home and school mathematics
• 6 Making sense of children’s mathematical graphics
• 7 Understanding children’s developing calculations
• 8 Environments that support children’s mathematical graphics
• 9 Case studies from early childhood settings
• 10 Developing children’s written methods
• 11 Involving parents and families
• 12 Children, teachers and possibilities
• Reflections
• Appendix: our research
• Glossary
• References
• Author Index
• Subject Index