An Elementary Approach to Design and Analysis of Algorithms

Lekh Raj Vermani, Shalini Vermani

• Publisher: WSPC (EUROPE)
• Year: 2019
• eBook ISBN: 9781786346773
• Topic: Ciencia de la computación
• Subtopic: Algoritmos de programación

In computer science, an algorithm is an unambiguous specification of how to solve a class of problems. Algorithms can perform calculation, data processing and automated reasoning tasks.

As an effective method, an algorithm can be expressed within a finite amount of space and time and in a well-defined formal language for calculating a function. Starting from an initial state and initial input (perhaps empty), the instructions describe a computation that, when executed, proceeds through a finite number of well-defined successive states, eventually producing 'output' and terminating at a final ending state. The transition from one state to the next is not necessarily deterministic; some algorithms, known as randomized algorithms, incorporate random input.

This book introduces a set of concepts in solving problems computationally such as Growth of Functions; Backtracking; Divide and Conquer; Greedy Algorithms; Dynamic Programming; Elementary Graph Algorithms; Minimal Spanning Tree; Single-Source Shortest Paths; All Pairs Shortest Paths; Flow Networks; Polynomial Multiplication, to ways of solving NP-Complete Problems, supported with comprehensive, and detailed problems and solutions, making it an ideal resource to those studying computer science, computer engineering and information technology.

Contents:

• Preface
• About the Authors
• Algorithms
• Growth of Functions
• Backtracking
• Divide and Conquer
• Greedy Algorithms
• Dynamic Programming
• Elementary Graph Algorithms
• Minimal Spanning Tree
• Single-Source Shortest Paths
• All Pairs Shortest Paths
• Flow Networks
• Polynomial Multiplication, FFT and DFT
• String Matching
• Sorting Networks
• NP-Complete Problems
• Bibliography
• Index

Readership: Students studying for degrees in computer science, computer engineering and information technology.Algorithms;Computer Science;Computer Engineering;Information Technology00

Chapter 1

Algorithms

In the subject of computer science the word algorithm, in general, refers to a method that can be used by a computer for the solution of a problem. As such the word algorithm does not simply mean a process, technique or method. Strictly speaking, it is a finite collection of well-defined computational techniques each of which is clear and unambiguous, capable of being performed with finite effort and terminates in a finite amount of time. Before an algorithm comes to play, a problem to be solved on computer is first converted into a mathematical problem called mathematical model. An algorithm is different from a program (computer program). Although algorithm is an easily understood procedure giving a set of logical instructions for solving the problem at hand, a program is written in a computer language giving the instructions that the computer understands.

1.1.Some Sorting Algorithms

We begin our study of algorithms by considering some sorting algorithms. Here we are given a sequence of non-negative integers a₁, a₂, . . . , a_n, not necessarily all distinct, the aim is to obtain a permutation of the a’s to get the numbers in a non-decreasing (or non-increasing) order i.e., to obtain a sequence a_1′, a_2′, . . . , a_n′ with {a_1′, a_2′, . . . , a_n′} = {a₁, a₂, . . . , a_n} and a_1′ ≤ a_2′ ≤

≤ a_n′. We restrict ourselves to obtaining a non-decreasing sequence.

1.1.1.Bubble sort

Among the sorting algorithms, this is most perhaps the easiest. In this algorithm a_n is first compared with a_n–1 and if a_n < a_n–1, a_n and a_n–1 are interchanged. Then a_n is compared with a_n–2 and if a_n < a_n–2, a_n and a_n–2 are interchanged and the process stops when we come to an a_i such that a_i < a_n. The process is then followed with a_n–1, then a_n–2 etc.

Algorithm 1.1. Bubble Sort Algorithm

1.For i = 1 to n − 1, do

2.forj = n to i + 1

3.if a_j < a_j–1, then

4.interchange (swap) a_j ↔ a_j–1

We will better explain this algorithm through two examples: one a sequence with all terms distinct and the other when all the terms are not necessarily distinct. We may not restrict ourselves to sequences of numbers alone but may consider sequences over any ordered set.

Example 1.1. Using bubble sort, rearrange the sequence

in alphabetical order.

Solution. This is a sequence of six terms all distinct. So i takes the values from 1 to 5. We express the sequence as a column denoting each word by the first letter of the word. We shall fully describe the internal loops for every i (refer to Table 1.1).

Observe that in the case i = 1, there is no change for j = 5, in the case of i = 2, there is no change for j = 6, 5, 4 and for i = 3, there is no change for j = 6, 5. At this stage the sequence is already sorted and, so, for i = 4 and 5, no changes are required. Hence the final sorted sequence is A, E, K, P, S, V or

Example 1.2. Using bubble sort, rearrange the sequence 2, 3, 6, 1, 0, 4, 8, 0 in non-decreasing order.

Table 1.1

Table 1.2(a)

Table 1.2(b)

Solution. This is a sequence of eight terms. So i takes values from 1 to 7. We express the sequence as a column and fully describe the internal loops for every i (as given in Tables 1.2(a) and 1.2(b)).

Observe that the array obtained in the last column of Table 1.2(b) is already sorted and, so, no changes are needed for i = 5, 6, 7. Also on the way, no changes were needed for i =...

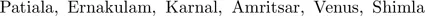
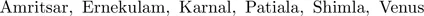
Table of contents

• Cover
• Halftitle
• Series Editors
• Title
• Copyright
• Dedication
• Preface
• Authors
• Contents
• Chapter 1. Algorithms
• Chapter 2. Growth of Functions
• Chapter 3. Backtracking
• Chapter 4. Divide and Conquer
• Chapter 5. Greedy Algorithms
• Chapter 6. Dynamic Programming
• Chapter 7. Elementary Graph Algorithms
• Chapter 8. Minimal Spanning Tree
• Chapter 9. Single-Source Shortest Paths
• Chapter 10. All Pairs Shortest Paths
• Chapter 11. Flow Networks
• Chapter 12. Polynomial Multiplication, FFT and DFT
• Chapter 13. String Matching
• Chapter 14. Sorting Networks
• Chapter 15. NP-Complete Problems
• Bibliography
• Index