Biomechanics in Orthodontics

Principles and Practice

Ram S. Nanda, Yahya S. Tosun

• Verlag: Quintessence Publishing Co, Inc
• Jahr: 2019
• ISBN:
  9780867156201
• Thema: Medicine
• Thema: Dentistry

Correct application of the principles of biomechanics leads to highly efficient and successful orthodontic treatment; a lack of proper understanding produces ineffectual systems that may even lead to collateral tissue damage. In addition, knowledge about the properties of the latest wire, bracket, and bonding materials and designs is a key factor in the configuration of successful orthodontic appliances. This essential book introduces students of orthodontics to the evolution of orthodontic technology and the properties of orthodontic materials and outlines the essential mechanical principles behind successful orthodontic treatment.

Physical Principles

Movement of teeth in orthodontic treatment requires application of forces and periodontal tissue response to these forces. Force mechanics are governed by physical principles, such as the laws of Newton and Hooke. This chapter presents the basic definitions, concepts, and applicable mechanical principles of tooth movement, laying the groundwork for subsequent chapters.

Newton’s Laws

Isaac Newton’s (1642–1727) three laws of motion, which analyze the relations between the effective forces on objects and their movements, are all applicable to clinical orthodontics.

The law of inertia

The law of inertia analyzes the static balance of objects. Every body in a state of rest or uniform motion in a straight line will continue in the same state unless it is compelled to change by the forces applied to it.

The law of acceleration

The law of acceleration states that the change in motion is proportional to the motive force that is applied. Acceleration occurs in the direction of the straight line in which the force is applied: a = F/m, where a = acceleration, F = force, and m = mass.

The law of action and reaction

The reaction of two objects toward each other is always equal and in an opposite direction. Therefore, to every action there is always an equal and opposite reaction.

Vectors

When any two points in space are joined, a line of action is created between these points. When there is movement from one of these points toward the other, a direction is defined. The magnitude of this force is called a vector, it is shown by the length of an arrow, and its point of application is shown with a point. For example, in Fig 1-1, the line of action of the force vector, which is applied by the labial arch of a removable appliance on the labial surface of the crown of the incisor, is horizontal. The direction is backward (ie, from anterior to posterior), and its amount is signified by the length of the arrow.

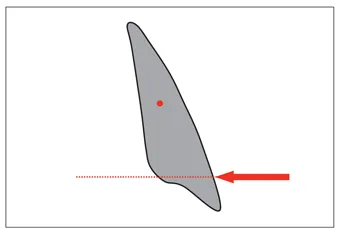
Fig 1-1 Force is a vector. The force applied to the incisor is signified by the length of the arrow, and the point of application is on the crown. Its line of action is horizontal, and its direction is from anterior to posterior.

Addition of vectors

Vectors are defined in a coordinate system. The use of two coordinate axes can be sufficient for vectors on the same plane.

In Fig 1-2a, the resultant (R) of the vectors of different forces (x and y), which are on the same line of action and in the same direction, equals the algebraic sum of these two vectors (x + y). The resultant of two vectors on the same line of action but in opposite directions can be calculated as (x + [–y]) (Fig 1-2b).

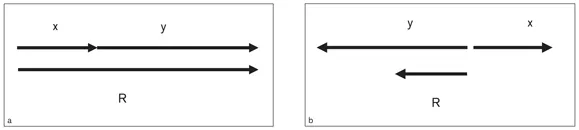
Fig 1-2 The resultant (R) of forces (x and y) on the same line of action and direction is R = x + y (a) and the same line of action but in different directions is R = x + (–y) (b).

The resultant of two vectors that have a common point of origin is the diagonal of a parallelogram whose sides are the two vectors (Fig 1-3a). The resultant of the same vectors can also be obtained by joining the tip of a vector parallel to vector y drawn from the tip of vector x to the point of origin of vector x (Fig 1-3b).

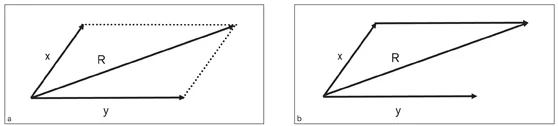
Fig 1-3 (a) The resultant (R) of the x and y vectors that have the same point of origin is the diagonal of the parallelogram with these vectors used as the sides. (b) R can also be obtained by drawing a vector parallel to vector y and extending from the tip of vector x, then drawing a line joining its tip to the origin of vector x.

Sum of multiple vectors

The sum of multiple vectors is calculated in the same system as the calculation of two vectors. Therefore, the third vector is added to the resultant of the first two vectors, and so on (Fig 1-4).

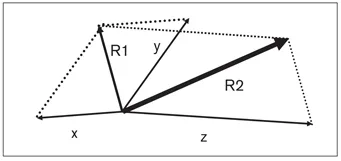
Fig 1-4 To find the sum of multiple vectors having the same point of origin, first draw the resultant (R1) of vectors x and y, thus defining the resultant (R2) of the z and R1 vectors (ie, x + y = R1; z + R1 = R2).

Subtraction of two vectors

To define the difference between two vectors, a new vector (–y) is drawn in the opposite direction from the tip of vector x and parallel to vector y, and the point of origin of vector x is joined to the tip of vector –y (Fig 1-5). Thus, the resultant (R) is from the point of origin of vectors x and y toward the tip of vector –y.

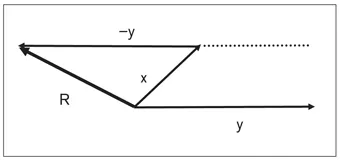
Fig 1-5 The difference between x and y vectors having the same point of origin can be obtained by drawing a vector (–y) starting from the tip of vector x that runs parallel to the y vector but in the opposite direction; then the tip of vector –y is joined to the point of origin of vectors x and y.

Separating a vector into components

To separate a resultant vector (R) into components, two parallel lines are drawn from the point of origin of that vector toward the components that are searched. By drawing parallels from the R vector’s tip toward these lines, a parallelogram is obtained. The sum of the two components obtained by this method is exactly equal to vector R.

The separation of a resultant vector into components is generally (at the elementary level) realized on x and y reference axes for ease of presentation and trigonometric calculations (Fig 1-6). In fact, for complicated calculations, vectors can be separated into unnumbered directions. Therefore, the x-axis is generally accepted as the horizontal axis, and the y-axis is accepted as the vertical axis. Thus, the component x of vector R can be defined as horizontal and the component y as vertical.

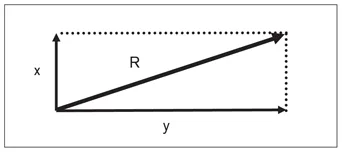
Fig 1-6 The separation of a resultant vector into components on an x- and y-axis coordinate system.

Force

Force is the effect that causes an object in space to change its place or its shape. In orthodontics, the force is measured in grams, ounces, or Newtons. Force is a vector having the characteristics of line of action, direction, magnitude, and point of application. In the application of orthodontic forces, some factors such as distribution and duration are also important. During tipping of a tooth, force is concentrated at the alveolar crest on one side and at the apex on the other (Fig 1-7a). During translation, however, the force is evenly distributed onto the bone and root surfaces (Fig 1-7b).

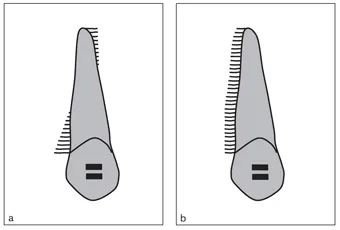
Fig 1-7 Distribution of force on the bone and root surfaces in tipping (a) and translatory (b) movements. During tipping, the possibility of indirect bone resorption is high because the forces are concentrated in small areas. Therefore, the forces must be kept as low as possible.

Forces according to their duration

Constancy of force

Clinically, optimal force is the amount of force resulting in the fastest tooth movement without damage to the periodontal tissues or discomfort to the patient. To achieve an optimum biologic response in the periodontal tissues, light, continuous force is important.¹ Figure 1-8 compares the amount of loss of force occurring over time on the force levels of two coil springs of high and low load/deflection rates.²

Continuous forces A continuous force can be obtained by using wires with low load/deflection rate and high working range. In the leveling phase, where there is considerable variation in level between teeth, it is advantageous to use these wires to control anchorage and maintain longer inte...