
eBook - ePub
Logics and Languages
Max Cresswell
This is a test
Buch teilen
- 284 Seiten
- English
- ePUB (handyfreundlich)
- Über iOS und Android verfügbar
eBook - ePub
Logics and Languages
Max Cresswell
Angaben zum Buch
Buchvorschau
Inhaltsverzeichnis
Quellenangaben
Über dieses Buch
Originally published in 1973, this book shows that methods developed for the semantics of systems of formal logic can be successfully applied to problems about the semantics of natural languages; and, moreover, that such methods can take account of features of natural language which have often been thought incapable of formal treatment, such as vagueness, context dependence and metaphorical meaning.
Parts 1 and 2 set out a class of formal languages and their semantics. Parts 3 and 4 show that these formal languages are rich enought to be used in the precise description of natural languages.
Appendices describe some of the concepts discussed in the text.
Häufig gestellte Fragen
Wie kann ich mein Abo kündigen?
Gehe einfach zum Kontobereich in den Einstellungen und klicke auf „Abo kündigen“ – ganz einfach. Nachdem du gekündigt hast, bleibt deine Mitgliedschaft für den verbleibenden Abozeitraum, den du bereits bezahlt hast, aktiv. Mehr Informationen hier.
(Wie) Kann ich Bücher herunterladen?
Derzeit stehen all unsere auf Mobilgeräte reagierenden ePub-Bücher zum Download über die App zur Verfügung. Die meisten unserer PDFs stehen ebenfalls zum Download bereit; wir arbeiten daran, auch die übrigen PDFs zum Download anzubieten, bei denen dies aktuell noch nicht möglich ist. Weitere Informationen hier.
Welcher Unterschied besteht bei den Preisen zwischen den Aboplänen?
Mit beiden Aboplänen erhältst du vollen Zugang zur Bibliothek und allen Funktionen von Perlego. Die einzigen Unterschiede bestehen im Preis und dem Abozeitraum: Mit dem Jahresabo sparst du auf 12 Monate gerechnet im Vergleich zum Monatsabo rund 30 %.
Was ist Perlego?
Wir sind ein Online-Abodienst für Lehrbücher, bei dem du für weniger als den Preis eines einzelnen Buches pro Monat Zugang zu einer ganzen Online-Bibliothek erhältst. Mit über 1 Million Büchern zu über 1.000 verschiedenen Themen haben wir bestimmt alles, was du brauchst! Weitere Informationen hier.
Unterstützt Perlego Text-zu-Sprache?
Achte auf das Symbol zum Vorlesen in deinem nächsten Buch, um zu sehen, ob du es dir auch anhören kannst. Bei diesem Tool wird dir Text laut vorgelesen, wobei der Text beim Vorlesen auch grafisch hervorgehoben wird. Du kannst das Vorlesen jederzeit anhalten, beschleunigen und verlangsamen. Weitere Informationen hier.
Ist Logics and Languages als Online-PDF/ePub verfügbar?
Ja, du hast Zugang zu Logics and Languages von Max Cresswell im PDF- und/oder ePub-Format sowie zu anderen beliebten Büchern aus Philosophie & Sprache in der Philosophie. Aus unserem Katalog stehen dir über 1 Million Bücher zur Verfügung.
Information
PART ONE
Propositional Languages
CHAPTER ONE
Syntax and Semantics of Propositional Languages
Our aim in this book will be to set out and discuss artificial languages which can exhibit many if not all of the semantical features of natural languages. Such an aim will necessitate a very general definition of a wide class of languages. Part I of the book will prepare the way by studying the general form of the languages of propositional logic, particularly the languages of intensional logic.
Syntax
By a propositional language ℒ we mean an ordered pair 〈Δ, S〉 where Δ = 〈Δ0, …, Δk〉 is a finite sequence of pairwise disjoint, possibly empty, finite sets, and S is the smallest set such that:
1.1 Δ0⊆S.1.2 If δ∈ Δn (1 ⩽ n ⩽ k) and α1…,αn ∈ S then 〈δ, α1…,αn〉 ∈ S.17
What the definition comes to is this. The union of all the sets in Δ, denoted by Δ+, is the set of symbols18 or words of ℒ and S is the set of sentences or (well-formed) formulae. Δ0 is the set of simple sentence symbols (for by 1.1 any member of Δ0 is a member of S, i.e., a sentence) and Δn (1 ≦ n ≦ k) is the set of n-place propositional functors. An n-place propositional functor is a symbol which when placed before n sentences forms another (complex) sentence. This is what 1.2 says. Those familiar with propositional logic, who may be finding all this rather too abstract, should think of the propositional calculus as a propositional language. Δ0 is the set of ‘propositional variables’, Δ1 contains one member, the symbol ~, Δ2 may contain the symbols ⊃, ∨, . , ≡ and perhaps a few others.19 In this case k = 2; and indeed most versions of the propositional calculus contain at most 2-place functors.
Other propositional logics (modal logics, e.g., with the symbols L and M, or □ and ◊ ; in Δ1) also fall under our definition. There is however one important restriction, that is that Δ0 is finite. In most propositional logics the simple sentence symbols are denumerably infinite and in some, e.g. PC itself, it is crucial that this should be so. There are not too complicated ways of achieving an infinite number of simple sentence symbols out of a finite alphabet (e.g. p, p′, p″, p‴, p″″ etc.) but they take us a little beyond the definition we have given.
The only restriction we have placed on the members of Δ+ is that they be finite and have no common members. This does not rule out the possibility that a complex sentence might also be a symbol. Suppose for instance that Δ0 = {α} and Δ1 = {δ, 〈δ, α〉}. Then Δ0 and Δ1 are disjoint but 〈δ, α〉 is both a functor and a complex sentence. Since this is undesirable for all sorts of reasons we shall say that a propositional language is grounded iff for no δ ∈ Δn and α1, …, αn ∈ S is 〈δ, α1, …, αn〉 ∈ Δ+. We shall assume that all the propositional languages we discuss are grounded.
Apart from these restrictions the members of Δ+ may be anything we please. At first this may seem a little strange. Since we speak about them as symbols shouldn’t we say what symbols are ? And since we talk about functors making complex sentences out of simpler ones shouldn’t we say something about how the putting together is done? The answer is that, fortunately, for the semantical analysis of a language we do not, at this stage at least, have to answer these questions. When we actually use a language of course the members of Δ+ can’t be just any old things. E.g., suppose Big Ben is a member of Δ0 and Walter Scott a member of Δ1, then the sequence (ordered pair) whose first member is Walter Scott and whose second Big Ben is a sentence of our language, and it is a little difficult to see how such a language would be any good in practice. For languages actually in use the symbols can perhaps be regarded as classes of utterances.20 We shall have a little more to say on this problem later: for the moment we simply repeat that symbols can be anything we like and that sentences are set-theoretical entities (sequences) made up out of the symbols according to 1.1 and 1.2.
The rules 1.1 and 1.2 may be regarded as specifying the syntax of propositional languages, for they determine the class of grammatically well-formed sentences of these languages. Before we proceed to semantics we shall describe these rules in a slightly different way which will lend itself to fairly easy generalization when we come to more elaborate languages. In describing a propositional language we make use of the notion of a syntactic category.21 In propositional languages one of these is the category of sentence, while the others are all categories of functors.
A functor is a symbol which, occurring as the first member of a sequence of symbols of certain syntactical kinds, makes a sequence of the same or another syntactical kind. If δ ∈ Δn then δ placed before n members of the category sentence forms another sequence of the category sentence.
In Chapter Five we shall use ‘F’ to denote a class of functors and use a subscript to indicate the kind of functor. We shall be using 0 to indicate the category of sentence. Since an n-place propositional functor forms a sentence, i.e. a thing of category 0, out of n other things of category 0 we can represent the class of n-place functors as
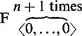
Here the ordered n + 1-tuple of 0’s may be said to be the category index of n-place propositional functors. The first member of the n + 1-tuple tells us that what is formed by the functor is a thing of category 0 and the last n members tell us that this is formed out of n other things of catego...