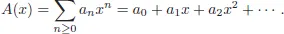Algebra, Logic and Combinatorics

Shaun Bullett, Tom Fearn;Frank Smith

• Verlag: WSPC (EUROPE)
• Jahr: 2016
• ISBN:
  9781786340320
• Thema: Matematica
• Thema: Algebra

This book leads readers from a basic foundation to an advanced level understanding of algebra, logic and combinatorics. Perfect for graduate or PhD mathematical-science students looking for help in understanding the fundamentals of the topic, it also explores more specific areas such as invariant theory of finite groups, model theory, and enumerative combinatorics.

Algebra, Logic and Combinatorics is the third volume of the LTCC Advanced Mathematics Series. This series is the first to provide advanced introductions to mathematical science topics to advanced students of mathematics. Edited by the three joint heads of the London Taught Course Centre for PhD Students in the Mathematical Sciences (LTCC), each book supports readers in broadening their mathematical knowledge outside of their immediate research disciplines while also covering specialized key areas.

Contents:

• Enumerative Combinatorics (Peter J Cameron)
• Introduction to the Finite Simple Groups (Robert A Wilson)
• Introduction to Representations of Algebras and Quivers (Anton Cox)
• The Invariant Theory of Finite Groups (P Fleischmann and R J Shank)
• Model Theory (I Tomašić)

Readership: Researchers, graduate or PhD mathematical-science students who require a reference book that covers algebra, logic or combinatorics.
Pure Mathematics;Applied Mathematics;Mathematical Sciences;Techniques;Algebra;Logic;Combinatorics;Fluid Dynamics;Solid Mechanics Key Features:

• Each chapter is written by a leading lecturer in the field
• Concise and versatile
• Can be used as a masters level teaching support or a reference handbook for researchers

Chapter 1

Enumerative Combinatorics

Peter J. Cameron

School of Mathematical Sciences,
Queen Mary University of London, London E1 4NS, UK^∗
[email protected]

This chapter presents a very brief introduction to enumerative combinatorics. After a section on formal power series, it discusses examples of counting subsets, partitions and permutations; techniques for solving recurrence relations; the inclusion–exclusion principle; the Möbius function of a poset; q-binomial coefficients; and orbit-counting. A section on the theory of species (introduced by André Joyal) follows. The chapter concludes with a number of exercises, some of which are worked.

1.Introduction

Combinatorics is the science of arrangements. We want to arrange objects according to certain rules, for example, digits in a sudoku grid. We can break the basic question into three parts:

•Is an arrangement according to the rules possible?

•If so, how many different arrangements are there?

•What properties (for example, symmetry) do the arrangements possess?

Enumerative combinatorics provides techniques for answering the second of these questions.

Unlike the case of sudoku, we are usually faced by an infinite sequence of problems indexed by a natural number n. So if a_n is the number of solutions to the problem with index n, then the solution of the problem is a sequence (a₀, a₁, . . .) of natural numbers. We combine these into a single object, a formal power series, sometimes called the generating function of the sequence. In the next section, we will briefly sketch the theory of formal power series.

For example, consider the problem:

Problem 1. How many subsets of a set of size n are there?

Of course, the answer is 2ⁿ. The generating function is

Needless to say, in most cases we cannot expect such a complete answer!

In the remainder of the chapter, we examine some special cases, treating some of the important principles of combinatorics (such as counting up to symmetry and inclusion–exclusion).

An important part of the subject involves finding good asymptotic estimates for the solution; this is especially necessary if there is no simple formula for it. Space does not permit a detailed account of this; see Flajolet and Sedgewick [4] or Odlyzko [10].

The chapter concludes with some suggestions for further reading.

To conclude this section, recall the definition of the binomial coefficients:

A familiar problem of elementary combinatorics asks for the number of ways in which k objects can be chosen from a set of n, under various combinations of sampling rules:

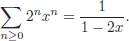
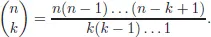
2.Formal Power Series

2.1.Definition

It is sometimes said that formal power series were the 19th-century analogue of random-access memory.

Suppose that (a₀, a₁, a₂, . . .) is an infinite sequence of numbers. We can wrap up the whole sequence into a single object, the formal power series A(x) in an indeterminate x given by

We have not lost any information, since the numbers a_n can be recovered from the power series:

Of course, we will have to think carefully about what is going on here, especially if the power series doesn’t converge, so that we cannot apply the techniques of analysis.

In fact, it is very important that our treatment should not depend on using analytic techniques. We define formal power series and operations on them abstractly, but at the end it is legitimate to think that formulae like the above are valid, and questions of convergence do not enter. So operations on formal power series are not allowed to involve infinite sums, for example; but finite sums are legitimate. The “coefficients” will usually be taken from some number system, but may indeed come from any commutative ring with identity.

Here is a brief survey of how it is done.

A formal power series is defined as simply a sequence (a_n)_n≥0; but keep i...