Argand Diagram

12 Key excerpts on "Argand Diagram"

• 

  eBook - ePub

  The Universal Book of Mathematics

  From Abracadabra to Zeno's Paradoxes

  • David Darling(Author)
  • 2008(Publication Date)
  • Trade Paper Press

    (Publisher)

  North American telephone area codes seem to have been chosen at random. But there was a method to their selection. In the mid-1950s when direct dialing of long-distance calls first became possible, it made sense to assign area codes that took the shortest time to dial to the larger cities. Almost all calls were from rotary dials. Area codes such as 212, 213, 312, and 313 took very little time for the dial to return to its starting position compared, for example, to numbers such as 809, 908, 709. The quickest-to-dial area codes were assigned to the places expected to receive the most direct-dialed calls. New York City got 212, Chicago 312, Los Angeles 213, and Washington, D.C., 202, which is a little longer to dial than 212, but much shorter than others. In order of decreasing size and estimated amount of telephone traffic, the numbers grew larger: San Francisco got 415, Miami 305, and so on. At the other end of the spectrum came places like Hawaii (the last state annexed in 1959) with 808, Puerto Rico with 809, and Newfoundland with 709. The original plan (still in use until about 1993) was that area codes had a certain construction to the numbers: the first digit is 2 through 9, the second digit is 0 or 1, and the third digit is 1 through 9. Three-digit numbers with two zeros are special codes, that is, 700, 800, or 900. Three-digit numbers with two ones are for special local codes such as 411 for local directory assistance, 611 for repairs, and so forth.

  Argand Diagram

  A way of representing complex number s as points on a coordinate plane, also known as the Argand plane or the complex plane , using the x -axis as the real axis and the y -axis as the imaginary axis. It is named for the French amateur mathematician Jean Robert Argand (1768–1822) who described it in a paper in 1806.

  [14 ]

  John Wallis suggested a similar method 120 years earlier and Casper Wessel extensively developed it. But Wessel’s paper was published in Danish and wasn’t circulated in the languages more common to mathematics at that time. In fact, it wasn’t until 1895 that his paper came to the attention of the mathematical community–long after the name “Argand Diagram” had stuck.

  argument

  (1) The input for a function . (2) The angle between ZO, where Z is the point representing a complex number on an Argand Diagram and O is the origin, and the real axis. (3) A mathematical proof, possibly an informal one.

  Aristotle’s wheel

  A paradox mentioned in the ancient Greek text Mechanica , whose author is unknown but is suspected by some to have been Aristotle. The paradox concerns two concentric circles on a wheel, as shown in the diagram. A one-to-one correspondence exists between points on the larger circle and those on the smaller circle. Therefore, the wheel should travel the same distance regardless of whether it is rolled from left to right on the top straight line or on the bottom one. This seems to imply that the two circumferences of the different-sized circles are equal, which is impossible. How can this apparent contradiction be resolved? The key lies in the (false) assumption that a one-to-one correspondence of points means that two curves must have the same length. In fact, the cardinalities of points in a line segment of any length (or even an infinitely long line or an infinitely large n -dimensional Euclidean space) are all the same. See also infinity

  Sign up to read

  Learn more about book
• 

  eBook - PDF

  A Course of Mathematics for Engineers and Scientists

  Volume 1

  • Brian H. Chirgwin, Charles Plumpton(Authors)
  • 2014(Publication Date)
  • Pergamon

    (Publisher)

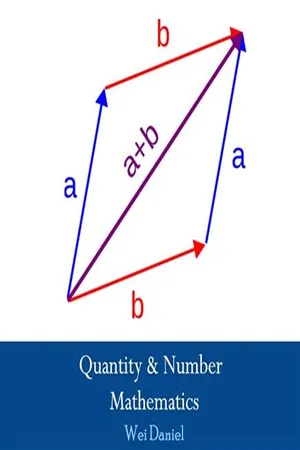
  A real number x may be represented by a point P on an infinite straight line when an origin 0 on the line has been chosen. The length O P is numerically equal to x and the sign of x decides whether P lies to the right, x > 0, or left, x < 0, of 0. A complex number z needs two real numbers x, y to define z — x + iy. The Argand Diagram represents 2 by a point P (2= x + iy) P FIG. 69. The Argand Diagram. in a plane whose rectangular coordinates (x, y) are the real and imaginary parts respectively of z, Fig. 69. The axis Ox is often called the real axis because the points on it represent numbers whose imaginary part is zero ; they are of the form x + iO. Similarly the axis Oy is the imaginary axis because the points on it correspond to numbers 0 + iy, i.e., pure imaginary numbers. We can now define the other terms we need by reference to the Argand Diagram. In Fig.69 where P represents z (= x + iy): (i) the modulus, z |, is a positive number equal to the length OP z = i(x 2 + y 2 ) = r (the modulus of a negative real number is a special case of this defini-tion) ; (ii) the argument (or amplitude) of z is the angle 0, taken to be positive when the rotation from Ox towards O P is in the anti-clockwise sense and we write arg z = Θ ; §7:1 COMPLEX N U M B E R S 265 (iii) the complex conjugate, z, is the number represented by the optical image of P in the real axis. .·. z = x z = z ly, arg z = —arg z, and zz — (x + iy)(x — iy) = x* + z/ 2 = |2| 2 . A ( 2 , + Z 2 ) FIG. 70. Addition of complex numbers. The quotient of two complex numbers can be expressed as a complex number by multiplying numerator and denominator by the conjugate of the denominator. Thus x 2 + iy 2 (x 2 + iy 2 )(x 1 - iy x ) iVi (*i + iyi)(Zi— il Ji) (x x x 2 + y t y 2 ) + ί(χ^ 2 — x 2 y x ) y The representation of addition on the Argand Diagram leads to a 'parallelogram law for the addition of two complex numbers, Fig. 70(a).

  Sign up to read

  Learn more about book
• 

  eBook - PDF

  Mathematical Methods

  A Course of Mathematics for Engineers and Scientists

  • Brian H. Chirgwin, Charles Plumpton(Authors)
  • 2014(Publication Date)
  • Pergamon

    (Publisher)

  A real number x may be represented by a point P on an infinite straight line when an origin O on the line has been chosen. The length OP is numer-ically equal to x and the sign of x decides whether P lies to the right, x > 0, or left, x < 0, of O. Two real numbers x, y are needed to define the complex number z = x+iy. The Argand Diagram, or z-plane, represents z by a point P in a plane whose rectangular coordinates (x, y) are the real and imaginary parts respectively of z, Fig. 7.1. (z = x + iy) P x FIG. 7.1. The Argand Diagram (z-plane). The axis Ox is often called the real axis because the points on it represent numbers .whose imaginary part is zero; they are of the form x+ iO. Similarly the axis Oy is the imaginary axis because the points on it correspond to numbers 0+iy, i.e. pure imaginary numbers. We can now define the other terms we need by reference to the Argand Diagram. In Fig. 7.1 where P represents z (= x+iy): (i) the modulus, | z |, is a positive number equal to the length OP 1*1 = V(x 2 +y 2 ) = r (the modulus of a negative real number is a special case of this definition); (ii) the argument (or amplitude) of z is the angle Θ between OP and Ox, taken to be positive when the rotation from Ox towards OP is in the anticlockwise sense and we write argz = 0; 410 A COURSE OF MATHEMATICS [CH. 7 (iii) the complex conjugate, z*, is the number represented by the optical image of P in the real axis. [In earlier editions the symbol z was used for z*.] z = x-y, argz z* = z and zz -argz, (x+iy)(x — y) — x 2 --y 2 = jz| 2 A( Zl +z 2 ) FIG. 7.2. Illustrating the addition of complex numbers. The quotient of two complex numbers can be expresssed as a complex number by multiplying numerator and denominator by the conjugate of the denominator.

  Sign up to read

  Learn more about book
• 

  No longer available |Learn more

  Pure Mathematics & Important Mathematical Concepts

  • (Author)
  • 2014(Publication Date)
  • Orange Apple

    (Publisher)

  A complex number can be viewed as a point or position vector in a two-dimensional Cartesian coordinate system called the complex plane or Argand Diagram, named after Jean-Robert Argand. The numbers are conventionally plotted using the real part as the horizontal component, and imaginary part as vertical (see Figure 1). These two values used to identify a given complex number are therefore called its Cartesian-, rectangular-, or algebraic form . Geometric interpretation of the operations The operations described algebraically above can be visualised using Argand Diagrams. X = A + B : The sum of two points A and B of the complex plane is the point X = A + B such that the triangles with vertices 0, A , B , and X , B , A , are congruent. Thus the addition of two complex numbers is the same as vector addition of two vectors. X = AB : The product of two points A and B is the point X = AB such that the triangles with vertices 0, 1, A , and 0, B , X , are similar. ________________________ WORLD TECHNOLOGIES ________________________ X = A *: The complex conjugate of a point A is the point X = A * such that the triangles with vertices 0, 1, A , and 0, 1, X , are mirror images of each other. These geometric interpretations allow problems of algebra to be translated into geometry. And, conversely, geometric problems can be examined algebraically. For example, the problem of the geometric construction of the 17-gon was by Gauss translated into the analysis of the algebraic equation x 17 = 1. Polar form Figure 2: The argument φ and modulus r locate a point on an Argand Diagram; r (cosφ + i sinφ) or re i φ are polar expressions of the point. The diagrams suggest various properties. Firstly, the distance of a point z from the origin (shown as r in Figure 2) is known as the modulus , absolute value , or magnitude , and written | z | .

  Sign up to read

  Learn more about book
• 

  No longer available |Learn more

  Basics of Number Mathematics

  • (Author)
  • 2014(Publication Date)
  • Learning Press

    (Publisher)

  A complex number can be viewed as a point or position vector in a two-dimensional Cartesian coordinate system called the complex plane or Argand Diagram, named after Jean-Robert Argand. The numbers are conventionally plotted using the real part as the horizontal component, and imaginary part as vertical (see Figure 1). These two values used to identify a given complex number are therefore called its Cartesian-, rectangular-, or algebraic form . Geometric interpretation of the operations The operations described algebraically above can be visualised using Argand Diagrams. ________________________ WORLD TECHNOLOGIES ________________________ X = A + B : The sum of two points A and B of the complex plane is the point X = A + B such that the triangles with vertices 0, A , B , and X , B , A , are congruent. Thus the addition of two complex num bers is the same as vector addition of two vectors. X = AB : The product of two points A and B is the point X = AB such that the triangles with vertices 0, 1, A , and 0, B , X , are similar. X = A *: The complex conjugate of a point A is the point X = A * such that the triangles with vertices 0, 1, A , and 0, 1, X , are mirror images of each other. These geometric interpretations allow problems of algebra to be translated into geometry. And, conversely, geometric problems can be examined algebraically. For example, the problem of the geometric construction of the 17-gon was by Gauss translated into the analysis of the algebraic equation x 17 = 1. ________________________ WORLD TECHNOLOGIES ________________________ Polar form Figure 2: The argument φ and modulus r locate a point on an Argand Diagram; r (cosφ + i sinφ) or re i φ are polar expressions of the point. The diagrams suggest various properties. Firstly, the distance of a point z from the origin (shown as r in Figure 2) is known as the modulus , absolute value , or magnitude , and written | z |.

  Sign up to read

  Learn more about book
• 

  eBook - ePub

  Introduction to Actuarial and Financial Mathematical Methods

  • Stephen Garrett(Author)
  • 2015(Publication Date)
  • Academic Press

    (Publisher)

  2 = ±1, which leads to a total of four roots

  z = ± 1 and ± i

  This particular quartic function is therefore seen to have four roots in the complex plane. The reader is invited to confirm that these are indeed roots. Note that this approach is in contrast to the factorization approach used previously which would require one to determine the factorization g (z ) = (z − 1)(z + 1)(z 2 + 1) and is much more difficult.

  8.4 Argand Diagrams and the Polar Form

  8.4.1 Polar form

  We have previously discussed the necessity of thinking of complex numbers as existing on a two-dimensional complex plane, as illustrated in Figure 8.1 . Until now, we have chosen to define a complex number as a point on the complex plane given by its real and imaginary components and this led to the idea of an Argand Diagram that uses co-ordinates analogous to a two-dimensional Cartesian plane. Although this analogy is useful for working with complex numbers under the action of addition and subtraction, where the independence of the real and imaginary components is preserved, it is not very useful for operations such as multiplication and division where the independence is not preserved. To this end, we now consider an alternative geometrical interpretation of complex numbers, the polar form .

  The polar form still considers a complex number as existing on a two-dimensional complex plane and so still requires two numbers to define it. However, rather than defining a horizontal and vertical position, the polar form specifies an angle measured from the positive horizontal axis, called the argument , and a radial distance from the origin, called the modulus . This is illustrated in Figure 8.4 .

  Figure 8.4 Argand Diagram for polar form of complex number z = 4 + 4i.

  Clearly the modulus, r , and argument, θ , are related to the real and imaginary components of a complex number through projections onto the horizontal and vertical axes. That is,

  a = r cos θ and b = r sin θ

  and so any complex number can be represented as

  Sign up to read

  Learn more about book
• 

  eBook - PDF

  Mathematics NQF3 SB

  TVET FIRST

  • M Van Rensburg, I Mapaling, M Trollope A Thorne(Authors)
  • 2017(Publication Date)
  • Macmillan

    (Publisher)

  i × i 2 6. 4 i × i 3 10. 2 i × i × 3 i 2 2. ( − i ) × 4 i 7. ( − i ) 2 × 4 i 3 11. 2 i 3 × i 7 3. 2 i + 4i 8. 3 i − 4 i 12. i 2 + i 4 − i 5 4. ( i 2 ) 2 9. 4 __ i 13. i 6 __ i + i 7 __ i 3 5. 12 i ___ 6 i 3 11 Module 1 Unit 1.3 Constructing Argand Diagrams to find and represent complex numbers in standard or rectangular form 1.3.1 ℂonstructing an Argand Diagram –1 –2 2 1 2 1 –1 –2 vertical axis horizontal axis 0 (1; 2) Pre-knowledge ℂartesian plane A Cartesian plane is a two-dimensional (2D) plane that consists of two axes, a vertical and horizontal axis. Each axis is divided up using equally- spaced markings according to a suitable scale. The axes intersect or cross each other at the point zero, which is known as the origin (O). The axes divide the plane into four equal parts called quadrants. Points called coordinates are plotted on the quadrants. From Figure 1.6, the coordinate (1; 2) represents a horizontal value of 1 and a vertical value of 2. Figure 1.6: A Cartesian plane Complex numbers can be represented on a Cartesian plane: l The real numbers are represented on the real axis, which is a horizontal number line. l The imaginary numbers are represented on the imaginary axis, which is the vertical number line. The area formed from the axes is called a complex plane (see Figure 1.7).The graphical representation of complex numbers in a complex plane is called an Argand Diagram . Example 1.10 Represent z 1 = 2 + 3 i and z 2 = − 2 − 3 i on an Argand Diagram. Solution: Step 1: Work out which points you need to plot. Remember that a complex number is made up of a real part and an imaginary part: ℂomplex number Real part Imaginary part z 1 = 2 + 3 i 2 3 i z 2 = − 2 − 3 i − 2 − 3 i Step 2: Draw the imaginary and real axes for the complex plane. Add equally spaced markings along each axes starting at 0 and going at least as high as the largest real or imaginary number you have.

  Sign up to read

  Learn more about book
• 

  No longer available |Learn more

  General Mathematics & Precalculus Analysis

  • (Author)
  • 2014(Publication Date)
  • Library Press

    (Publisher)

  ________________________ WORLD TECHNOLOGIES ________________________ Chapter 7 Complex Number A complex number can be visually represented as a pair of numbers forming a vector on a diagram called an Argand Diagram, representing the complex plane. A complex number is a number consisting of a real and imaginary part. It can be written in the form a + bi , where a and b are real numbers, and i is the standard imaginary unit with the property i 2 = −1. The complex numbers contain the ordinary real numbers, but extend them by adding in extra numbers and correspondingly expanding the understanding of addition and multiplication. Complex numbers were first conceived and defined by the Italian mathematician Gerolamo Cardano, who called them fictitious, during his attempts to find solutions to cubic equations. The solution of a general cubic equation in radicals (without trigonometric functions) may require intermediate calculations containing the square roots of negative numbers, even when the final solutions are real numbers, a situation known as casus irreducibilis. This ultimately led to the fundamental theorem of algebra, which shows that with complex numbers, a solution exists to every polynomial equation of degree one or higher. Complex numbers thus form an algebraically closed field, where any polynomial equation has a root. The rules for addition, subtraction, multiplication, and division of complex numbers were developed by the Italian mathematician Rafael Bombelli. A more abstract formalism for the complex numbers was further developed by the Irish mathematician William Rowan Hamilton, who extended this abstraction to the theory of quaternions. ________________________ WORLD TECHNOLOGIES ________________________ Complex numbers are used in a number of fields, including: engineering, electro-magnetism, quantum physics, applied mathematics, and chaos theory.

  Sign up to read

  Learn more about book
• 

  No longer available |Learn more

  Complex Analysis & Key Mathematical Concepts (Concepts & Applications)

  • (Author)
  • 2014(Publication Date)
  • Orange Apple

    (Publisher)

  ________________________ WORLD TECHNOLOGIES ________________________ Chapter- 2 Complex Number A complex number can be visually represented as a pair of numbers forming a vector on a diagram called an Argand Diagram, representing the complex plane. A complex number is a number consisting of a real and imaginary part. It can be written in the form a + bi , where a and b are real numbers, and i is the standard imaginary unit with the property i 2 = −1. The complex numbers contain the ordinary real numbers, but extend them by adding in extra numbers and correspondingly expanding the understanding of addition and multiplication. Complex numbers were first conceived and defined by the Italian mathematician Gerolamo Cardano, who called them fictitious, during his attempts to find solutions to cubic equations. The solution of a general cubic equation in radicals (without trigonometric functions) may require intermediate calculations containing the square roots of negative numbers, even when the final solutions are real numbers, a situation known as casus irreducibilis. This ultimately led to the fundamental theorem of algebra, which shows that with complex numbers, a solution exists to every polynomial equation of degree one or higher. Complex numbers thus form an algebraically closed field, where any polynomial equation has a root. The rules for addition, subtraction, multiplication, and division of complex numbers were developed by the Italian mathematician Rafael Bombelli. A more abstract formalism for the complex numbers was further developed by the Irish mathematician William Rowan Hamilton, who extended this abstraction to the theory of quaternions. ________________________ WORLD TECHNOLOGIES ________________________ Complex numbers are used in a number of fields, including: engineering, electromagnetism, quantum physics, applied mathematics, and chaos theory.

  Sign up to read

  Learn more about book
• 

  No longer available |Learn more

  Quantity & Number Mathematics

  • (Author)
  • 2014(Publication Date)
  • Learning Press

    (Publisher)

  ________________________ WORLD TECHNOLOGIES ________________________ Chapter 4 Complex Number A complex number can be visually represented as a pair of numbers forming a vector on a diagram called an Argand Diagram, representing the complex plane. A complex number is a number consisting of a real and imaginary part. It can be written in the form a + bi , where a and b are real numbers, and i is the standard imaginary unit with the property i 2 = −1. The complex numbers contain the ordinary real numbers, but extend them by adding in extra numbers and correspondingly expanding the und-erstanding of addition and multiplication. Complex numbers were first conceived and defined by the Italian mathematician Gerolamo Cardano, who called them fictitious, during his attempts to find solutions to cubic equations. The solution of a general cubic equation in radicals (without trig-onometric functions) may require intermediate calculations containing the square roots of negative numbers, even when the final solutions are real numbers, a situation known as casus irreducibilis. This ultimately led to the fundamental theorem of algebra, which shows that with complex numbers, a solution exists to every polynomial equation of degree one or higher. Complex numbers thus form an algebraically closed field, where any polynomial equation has a root. The rules for addition, subtraction, multiplication, and division of complex numbers were developed by the Italian mathematician Rafael Bombelli. A more abstract formalism for ________________________ WORLD TECHNOLOGIES ________________________ the complex numbers was further developed by the Irish mathematician William Rowan Hamilton, who extended this abstraction to the theory of quaternions. Complex numbers are used in a number of fields, including: engineering, electro-magnetism, quantum physics, applied mathematics, and chaos theory.

  Sign up to read

  Learn more about book
• 

  No longer available |Learn more

  Introduction to Precalculus Analysis, An

  • (Author)
  • 2014(Publication Date)
  • Learning Press

    (Publisher)

  ________________________ WORLD TECHNOLOGIES ________________________ Chapter 2 Complex Number A complex number can be visually represented as a pair of numbers forming a vector on a diagram called an Argand Diagram, representing the complex plane. A complex number is a number consisting of a real and imaginary part. It can be written in the form a + bi , where a and b are real numbers, and i is the standard imaginary unit with the property i 2 = −1. The complex numbers contain the ordinary real numbers, but extend them by adding in extra numbers and correspondingly expanding the understanding of addition and multiplication. Complex numbers were first conceived and defined by the Italian mathematician Gerolamo Cardano, who called them fictitious, during his attempts to find solutions to cubic equations. The solution of a general cubic equation in radicals (without trigo-nometric functions) may require intermediate calculations containing the square roots of negative numbers, even when the final solutions are real numbers, a situation known as casus irreducibilis. This ultimately led to the fundamental theorem of algebra, which shows that with complex numbers, a solution exists to every polynomial equation of degree one or higher. Complex numbers thus form an algebraically closed field, where any polynomial equation has a root. The rules for addition, subtraction, multiplication, and division of complex numbers were developed by the Italian mathematician Rafael Bombelli. A more abstract formalism for the complex numbers was further developed by the Irish mathematician William Rowan Hamilton, who extended this abstraction to the theory of quaternions. ________________________ WORLD TECHNOLOGIES ________________________ Complex numbers are used in a number of fields, including: engineering, electro-magnetism, quantum physics, applied mathematics, and chaos theory.

  Sign up to read

  Learn more about book
• 

  eBook - ePub

  Higher Engineering Mathematics

  • John Bird(Author)
  • 2017(Publication Date)
  • Routledge

    (Publisher)

  He privately published a landmark essay on the representation of imaginary quantities which became known as the Argand Diagram. To find out more go to www.routledge.com/cw/bird and (2 + j 3) − (3 − j 4) = 2 + j 3 − 3 + j 4 = − 1 + j 7 The addition and subtraction of complex numbers may be achieved graphically as shown in the Argand Diagram of Fig. 22.2. (2 + j 3) is represented by vector OP and (3 − j 4) by vector OQ. In Fig. 22.2 (a) by vector addition (i.e. the diagonal of the parallelogram) OP + OQ = OR. R is the point (5, − j 1) Hence (2 + j 3) + (3 − j 4) = 5 − j 1 Figure 22.2 In Fig. 22.2 (b), vector OQ is reversed (shown as OQ ′) since it is being subtracted. (Note OQ = 3 − j 4and OQ ′ = −(3 − j 4) = −3 + j 4) OP − OQ = OP + OQ ′ = OS is found to be the Argand point (−1, j 7) Hence (2 + j 3) − (3 − j 4) = −1 + j 7 Problem 4. Given Z 1 = 2 + j 4 4and Z 2 = 3 − j determine (a) Z 1 + Z 2,    (b) Z 1 − Z 2,(c) Z 2 − Z 1 and show the results on an Argand Diagram. Z 1 + Z 2 = (2 + j 4) + (3 − j) = (2 + 3). + j (4 − 1) = 5 + j 3 Z 1 − Z 2 = (2 + j 4) − (3 − j) = (2 − 3) + j (4 − (−1)) = − 1 + j 5 Z 2 − Z 1 = (3 − j) − (2 + j 4) = (3 − 2) + j (−1 −4) = 1 − j 5 Each result is shown in the Argand Diagram of Fig. 22.3. Figure 22.3 22.4 Multiplication and division of complex numbers Multiplication of complex numbers is achieved by assuming all quantities involved are real and then using J 2 = −1 to simplify. Hence = a c + a (j d) + (j b) c + (j b) (j d) = a c + j a d + j b c + j 2 b d = (a c − b d) + j (a d + b c), since j 2 =. −1 Thus (3 + j 2) (4 − j 5) = 12 − j 15 + j 8 − j 2 10 = (12 − (− 10)) + j (− 15 + 8) = 2 2 − j 7 The complex conjugate of a complex number is obtained by changing the sign of the imaginary part. Hence the complex conjugate of a + jb is a − jb

  Sign up to read

  Learn more about book