Physics
Hooke's Law
Hooke's Law states that the force needed to extend or compress a spring by some distance is proportional to that distance. Mathematically, it is expressed as F = kx, where F is the force, k is the spring constant, and x is the displacement. This law is fundamental in understanding the behavior of elastic materials and is widely used in engineering and physics.
Written by Perlego with AI-assistance
Related key terms
1 of 5
4 Key excerpts on "Hooke's Law"
- eBook - PDF
- Mumtaz Kassir, Richard B. Hetnarski, Józef Ignaczak(Authors)
- 2016(Publication Date)
- CRC Press(Publisher)
The theory was concisely presented in a short sentence “Ut tensio sic vis; that is, The Power of any spring is in the same proportion with the Tension thereof.” He published this discovery at the end of his earlier Book of the Description of Helioscopes as an anagram, stated in this book in Section 3.3.1. By a “spring” Hooke did not mean a helical wire but any extensible body that returns to its original shape when the forces were removed. Although Hooke’s theory was one-dimensional, the present-day six relations between components of the stress tensor and the strain tensor are referred to as the generalized Hooke’s law. Apparently, the first to apply Hooke’s law to Galileo’s problem was Edmé Mariotte (1620–1684). Mariotte lived most of his life in Dijon, France. In 1666, he became a member of the French Academy of Sciences. He is credited with the introduction of experimental methods in France. As a result of his experiments with air, the Boyle–Mariotte law was established. Mariotte discovered Hooke’s law independently in 1680. In his work [3], he pointed out the fact that in a loaded beam, some fibers extended while other contracted. Unfortunately, he went somewhat too far in stating that half of the fibers were in each category. His contribution to the theory of elasticity came as a result of his work on the design of water pipelines for the Palace de Versailles. His experiments on wood and glass rods showed that Galileo’s theory gave values of a breaking force too large, so he developed his own theory, which included elastic properties of material. He analyzed not only cantilever beams but also beams on two supports and beams built in at both ends. ∗ The results of Mariotte’s experiments brought a few others to the field, espe- cially Gottfried Wilhelm Leibniz (1646–1716) [5] and, somewhat later, Pierre Varignon (1654–1722) [6], a French mathematician born in Caen in Normandy, a friend of Leibniz, Newton, and the members of the Bernoulli family. - Georgy V. Kostin, Vasily V. Saurin(Authors)
- 2012(Publication Date)
- De Gruyter(Publisher)
The results of numerous investigations have validated the correctness of Hooke’s law for many real materials, and the limiting deformations where the linear strain-stress relations are reliable have been estimated. These deformations change in a wide range of values from one material to another. While, for example, steel obeys Hooke’s law in a relatively wide band of loading parameters, such materials as cast iron deviate from the linear behavior even at relatively small stresses. In accordance with Cauchy [12], the generalized Hooke’s law can be presented as a linear relation between stress and strain tensors in the form D C.x/ W ; (2.55) where C is the elastic modulus tensor of the fourth rank. The components of the ten-sor C do not depend on the spatial coordinates in the case of homogeneous media. As the stress and strain components depend on the orientation of the Cartesian coor-dinate system, the components of the elastic modulus tensor must also comply with this dependence. These moduli are invariant with respect to arbitrary rotation of the coordinate system only in the case of isotropic material. The strain-stress relation (2.55) can be considered as the linear term of expansion in series of some general nonlinear function D ./ . It can be shown that there are nine relations in eq. (2.55) with nine terms each. Thus the tensor C has 81 com-ponents. Due to the symmetry of the tensors and , the number of independent equations decreases to six, and, consequently, because of the symmetry properties C ijkl D C jikl D C ij l k D C jilk ; i;j;k;l D 1;2;3; (2.56) the elastic modulus tensor has no more than 36 independent components. The matrix- eBook - ePub
- Shutilov, Vladimir Alexandrovich Shutilov, Yelena Vladimirovna Tcharnaya(Authors)
- 2020(Publication Date)
- CRC Press(Publisher)
The generalized Hooke’s law can then be formulated as follows: the components of the stress at a given point of the body are linear and homogeneous functions of all components of the strain, i.e. , σ 1 = c 1 1 ϵ 1 + c 1 2 ϵ 2 + c 13 ϵ 3 + c 14 ϵ 4 + c 15 ϵ 5 + c 1 6 ϵ 6 ; σ 2 = c 21 ϵ 1 + c 22 ϵ 2 + c 23 ϵ 3 + c 24 ϵ 4 + c 25 ϵ 5 + c 2 6 ϵ 6 ; σ 3 = c 31 ϵ 1 + c 32 ϵ 2[--. =PLGO-SEPARATOR=--]+ c 33 ϵ 3 + c 34 ϵ 4 + c 35 ϵ 5 + c 36 ϵ 6 ; σ 4 = c 41 ϵ 1 + c 42 ϵ 2 + c 43 ϵ 3 + c 44 ϵ 4 + c 45 ϵ 5 + c 46 ϵ 6 ; σ 5 = c 51 ϵ 1 + c 52 ϵ 2 + c 53 ϵ 3 + c 54 ϵ 4 + c 55 ϵ 5 +[-. -=PLGO-SEPARATOR=--]c 56 ϵ 6 ; σ 6 = c 61 ϵ 1 + c 62 ϵ 2 + c 63 ϵ 3 + c 64 ϵ 4 + c 65 ϵ 5 + c 66 ϵ 6 ; (I.13a) or, in general (matrix) form, σ n = c n m ϵ m, n, m = 1, 2, 3, 4, 5, 6 (I.13b) where summation over the repeated (dummy) index (the row index) is implied. In tensor form, when two indices must be retained for the components of the stresses and strains (as, for example, in the equation of motion (I.11)), the generalized Hooke’s law will have the form: σ i k = c iklj ϵ i j, (I.13c) The coefficients of proportionality c nm are called the linear elastic moduli or stiffness constants. Their dimensions are the same as the dimensions of stress; the 36 quantities c nm form a tensor of rank 4, called the elastic modulus tensor. In the theory of elasticity, it is shown 6, 7 that this tensor is symmetric, i.e. , c nm = c nm (c ikjl = c jlki), so that it contains 21 independent constants and has the. form c n m = [ c 11 c 12 c 13 c 14 c 15 c 16 c 12 c 22 c 23 c 24 c 25 c 26 c 13 c 32 c 33 c 34 c 35 c 36 c 14 c 42 c 43 c 44 c 45 c 46 c 15 c 52 c 53 c 54 c 55 c 56 c 16 c 62 c 63 c 64 c 65 c 66 ]. In this form, the. tensor c nm describes the elasticity of a medium without symmetry. The existence of symmetry reduces the total number of nonzero elastic moduli and the number of independent moduli. Table 1 shows the matrices of the elastic moduli for different crystallographic systems - Luis Manuel Braga da Costa Campos(Author)
- 2012(Publication Date)
- CRC Press(Publisher)
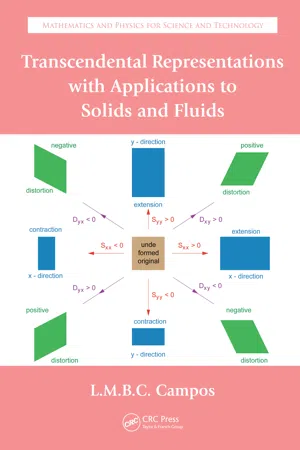
4.3.3 Direct and Inverse Hooke Law The Hooke law or stress–strain relation for an elastic medium states that the total stress is the sum of (1) those associated (Equation 4.65b) with the sliding tensor (Equations 4.63a and 4.63b); and (2) those due to volume changes (Equation 4.60b). It follows that (1) the shear stresses are propor-tional to the corresponding distortions (Equation 4.66b ≡ Equation 4.65b) through the shear modu-lus that is positive (Equation 4.65a ≡ Equation 4.66a): μ μ > { } = { } = { } 0 2 3 3 3 3 3 3 : T T T T T T S S S xy x y xy x y xy x y , , , , , , ; (4.66a and 4.66b) ν > { } = + + + { } 0 33 33 33 : T T T T T T T T T xx yy xx xx yy yy , , , , = { } + + + 2 33 μ ν S S S S S S xx yy xx yy , , 33 33 2 2 3 ( ) = { } + -μ ν μ S S S xx yy , , + + ( ) = + S S S xx yy 33 4 3 ν μ { } + - + + S S S S S S S xx yy yy xx , , , 33 33 33 2 3 ν μ , S S xx yy + { } ; (4.66c and 4.66d) 233 Plane Elasticity and Multiharmonic Functions and (2) the normal stresses (tractions/compressions) are due (Equation 4.66d) to the corresponding (Equation 4.65b) normal strains (extensions/contractions) through the modulus of sliding (Equation 4.65a) plus the volume changes (Equation 4.62b) through the volume modulus, which is also posi-tive (Equation 4.62b ≡ Equation 4.66c). The direct (inverse) Hooke law specifies stresses from strains (Equations 4.66a through 4.66d) [vice versa, i.e., the strains from the stresses (Equations 4.67a through 4.67c)]: 2 μ { S xy , S x 3 , S y 3 } = { T xy , T x 3 , T y 3 }, (4.67a) 2 1 2 3 33 33 μ μ ν S S S T T T T T xx yy xx yy xx , , , , { } = { } -- + yy T + 33 3 , (4.67b) 6 2 1 3 1 2 3 33 33 μ μ ν μ S S S T T T xx yy xx yy , , , , { } = + { } --ν + + + + { } T T T T T S yy xx xx yy 33 33 , , .
Index pages curate the most relevant extracts from our library of academic textbooks. They’ve been created using an in-house natural language model (NLM), each adding context and meaning to key research topics.