
- 414 pages
- English
- ePUB (mobile friendly)
- Available on iOS & Android
eBook - ePub
Partial Differential Equations for Scientists and Engineers
About this book
Most physical phenomena, whether in the domain of fluid dynamics, electricity, magnetism, mechanics, optics, or heat flow, can be described in general by partial differential equations. Indeed, such equations are crucial to mathematical physics. Although simplifications can be made that reduce these equations to ordinary differential equations, nevertheless the complete description of physical systems resides in the general area of partial differential equations.
This highly useful text shows the reader how to formulate a partial differential equation from the physical problem (constructing the mathematical model) and how to solve the equation (along with initial and boundary conditions). Written for advanced undergraduate and graduate students, as well as professionals working in the applied sciences, this clearly written book offers realistic, practical coverage of diffusion-type problems, hyperbolic-type problems, elliptic-type problems, and numerical and approximate methods. Each chapter contains a selection of relevant problems (answers are provided) and suggestions for further reading.
This highly useful text shows the reader how to formulate a partial differential equation from the physical problem (constructing the mathematical model) and how to solve the equation (along with initial and boundary conditions). Written for advanced undergraduate and graduate students, as well as professionals working in the applied sciences, this clearly written book offers realistic, practical coverage of diffusion-type problems, hyperbolic-type problems, elliptic-type problems, and numerical and approximate methods. Each chapter contains a selection of relevant problems (answers are provided) and suggestions for further reading.
Frequently asked questions
Yes, you can cancel anytime from the Subscription tab in your account settings on the Perlego website. Your subscription will stay active until the end of your current billing period. Learn how to cancel your subscription.
No, books cannot be downloaded as external files, such as PDFs, for use outside of Perlego. However, you can download books within the Perlego app for offline reading on mobile or tablet. Learn more here.
Perlego offers two plans: Essential and Complete
- Essential is ideal for learners and professionals who enjoy exploring a wide range of subjects. Access the Essential Library with 800,000+ trusted titles and best-sellers across business, personal growth, and the humanities. Includes unlimited reading time and Standard Read Aloud voice.
- Complete: Perfect for advanced learners and researchers needing full, unrestricted access. Unlock 1.4M+ books across hundreds of subjects, including academic and specialized titles. The Complete Plan also includes advanced features like Premium Read Aloud and Research Assistant.
We are an online textbook subscription service, where you can get access to an entire online library for less than the price of a single book per month. With over 1 million books across 1000+ topics, we’ve got you covered! Learn more here.
Look out for the read-aloud symbol on your next book to see if you can listen to it. The read-aloud tool reads text aloud for you, highlighting the text as it is being read. You can pause it, speed it up and slow it down. Learn more here.
Yes! You can use the Perlego app on both iOS or Android devices to read anytime, anywhere — even offline. Perfect for commutes or when you’re on the go.
Please note we cannot support devices running on iOS 13 and Android 7 or earlier. Learn more about using the app.
Please note we cannot support devices running on iOS 13 and Android 7 or earlier. Learn more about using the app.
Yes, you can access Partial Differential Equations for Scientists and Engineers by Stanley J. Farlow in PDF and/or ePUB format, as well as other popular books in Mathematics & Differential Equations. We have over one million books available in our catalogue for you to explore.
Information
PART 1
Introduction
LESSON 1
Introduction to Partial Differential Equations
PURPOSE OF LESSON: To show what partial differential equations are, why they are useful, and how they are solved; also included is a brief discussion on how they are classified as various kinds and types. An overview is given of many of the ideas that will be studied in detail later.
Most physical phenomena, whether in the domain of fluid dynamics, electricity, magnetism, mechanics, optics, or heat flow, can be described in general by partial differential equations (PDEs); in fact, most of mathematical physics are PDEs. It’s true that simplifications can be made that reduce the equations in question to ordinary differential equations, but, nevertheless, the complete description of these systems resides in the general area of PDEs.
What Are PDEs?
A partial differential equation is an equation that contains partial derivatives. In contrast to ordinary differential equations (ODEs), where the unknown function depends only on one variable, in PDEs, the unknown function depends on several variables (like temperature u(x,t) depends both on location x and time t).
Let’s list some well-known PDEs; note that for notational simplicity we have called
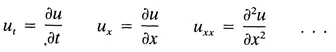
A Few Well-Known PDEs
| u, = uxx | (heat equation in one dimension) |
| ut = uxx + uyy | (heat equation in two dimensions) |
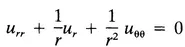 | (Laplace’s equation in polar coordinates) |
| utt = uxx + uyy + uzz | (wave equation in three dimensions) |
| utt = uxx + αut + βu | (telegraph equation) |
Note on the Examples
The unknown function u always depends on more than one variable. The variable u (which we differentiate) is called the dependent variable, whereas the ones we differentiate with respect to are called the independent variables. For example, it is clear from the equation
ut = uxx
that the dependent variable u(x,t) is a function of two independent variables ϰ and t, whereas in the equation
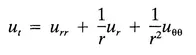
u(r, θ, t) depends on r, θ, and t.
Why Are PDEs Useful?
Most of the natural laws of physics, such as Maxwell’s equations, Newton’s law of cooling, the Navier-Stokes equations, Newton’s equations of motion, and Schrodinger’s equation of quantum mechanics, are stated (or can be) in terms of PDEs, that is, these laws describe physical phenomena by relating space and time derivatives. Derivatives occur in these equations because the derivatives represent natural things (like velocity, acceleration, force, friction, flux, current). Hence, we have equations relating partial derivatives of some unknown quantity that we would like to find.
The purpose of this book is to show the reader two things
- How to formulate the PDE from the physical problem (constructing the mathematical model).
- How to solve the PDE (along with initial and boundary conditions).
We wait a few lessons before we start the modeling problem; now, a brief overview on how PDEs are solved.
How Do You Solve a Partial Differential Equation?
This is a good question. It turns out that there is an entire arsenal of methods available to the practitioner; the most important methods are those that change PDEs into ODEs. Ten useful techniques are
- Separation of Variables. This technique reduces a PDE in n variables to n ODEs.
- Integral Transforms. This procedure reduces a PDE in n independent variables to one in n – 1 variables; hence, a PDE in two variables could be changed to an ODE.
- Change of Coordinat...
Table of contents
- Title Page
- Copyright Page
- Preface
- Table of Contents
- PART 1 - Introduction
- PART 2 - Diffusion-Type Problems
- PART 3 - Hyperbolic-Type Problems
- PART 4 - Elliptic-Type Problems
- PART 5 - Numerical and Approximate Methods
- ANSWERS TO SELECTED PROBLEMS
- APPENDIX 1 - Integral Transform Tables
- APPENDIX 2 - PDE Crossword Puzzle
- APPENDIX 3 - Laplacian in Different Coordinate Systems
- APPENDIX 4 - Types of Partial Differential Equations
- Index
- A CATALOG OF SELECTED DOVER BOOKS IN SCIENCE AND MATHEMATICS