The Soft Drinks Companion

A Technical Handbook for the Beverage Industry

Maurice Shachman

• Publisher: CRC Press
• Year: 2004
• Print ISBN: 9780849327261
• eBook ISBN: 9781135485399
• Topic: Technology & Engineering
• Subtopic: Food Science
• Index: Technology & Engineering

This comprehensive book presents key issues in the technology of the soft drinks industry. Employing a user-friendly format and writing style, the author draws on more than thirty-five years' hands-on experience in technical management in the soft drinks industry. The diverse subjects discussed focus on key scientific and technical issues encounter

1
Brix—The Basics

THE BRIX CONCEPT

I chose this subject for the first chapter in the handbook because Brix is one of the most pivotal technical topics encountered in the soft drinks industry. Generally, Brix (pronounced “bricks”) is used to indicate the amount of dissolved solids in a solution. In the soft drinks industry, it is used specifically to quantify the sugar in a beverage, syrup, or juice.

The Brix scale of measurement was established by a 19th century German chemist, Professor A.F.W.Brix, in whose honor the system is named. He found that by immersing a hydrometer in a fruit juice, he was able, from its density, to calculate the percentage of sugar in the juice. The Brix hydrometer was designed with a measurement scale from which fairly accurate sugar content was immediately readable. This was a boon to the European winemakers of the time, as they could assess the sugar content of grape juices and, thus, judge ahead the quality of the wine these could yield.

For Brix purposes in soft drinks technology, all dissolved solids are considered as sugar.

For the purpose of this handbook, Brix is defined as the percentage of dissolved sugar in a water solution on a weight for weight basis and is expressed in degrees Brix (°B). Thus, for example, a 10°B solution implies that in 100 g of solution, there are 10 g of dissolved sugar.

Note: The term “mass” is often confused with “weight.” Though there is a clear subtle scientific difference between these two terms, “weight” is loosely used when “mass” is intended. In this handbook, “weight” will occasionally also be loosely used, as it is the preferred term in parlance on the floor of a soft drink manufacturing facility.

Special note must be taken of the following fact: In a soft drink, there are, in addition to the sugar, other dissolved solids. They are in extremely small quantities compared to the sugar content but, nevertheless, contribute slightly to the Brix measurement. For pure convenience sake, we consider these to be “sugar” as well, that is, as far as the Brix reading is concerned. The very small error that can be introduced individually by a variety of different dissolved ingredients in different formulations is accepted on a universal basis and is ignored most of the time.

So then, in the soft drinks industry, all products, beverages, syrups, juices, etc., are considered as pure sugar solutions as far as Brix measurements are concerned. There are instances where this error must not be ignored, and these will be dealt with in specific sections of the handbook.

DENSITY

Brix is nothing more than the measurement of the density of a liquid. Density is defined as the weight of a specified volume of the liquid.

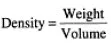
It is common to measure the weight in kilograms and the volume in liters. Therefore, as an example, if 1 liter of a sugar solution S weighs 1.034 kg, then it will have a density value of 1.034. (This, by the way, is equivalent to a Brix of about 9.20° B).

Though the Brix hydrometer in the soft drinks industry has been replaced by more sophisticated electronic and optical instruments, the manner in which it measures sugar content will help to understand the relationship of Brix to density.

Figure 1.1 describes the structure of a Brix hydrometer. The Brix hydrometer works on the Archimedes principle of buoyancy, which, simply stated, says:

A body immersed in a liquid will displace a volume of the liquid equal in weight to the weight of that body.

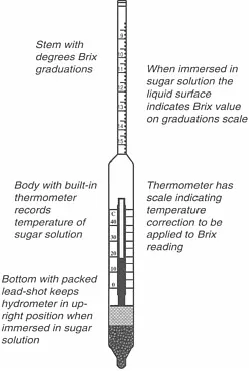
FIGURE 1.1 The Brix hydrometers.

Now imagine two sugar solutions in water, A and B. Let us say that in 1 liter of solution A there are 100 g of dissolved sugar. In 1 liter of solution B, there are 200 g. Sugar is heavier than water. Having more dissolved sugar and less water, solution B will be denser than solution A—it is “heavier” than solution A.

When the Brix hydrometer is placed in solution A, it will displace a volume of solution equal to its weight, which we will call W, and will sink to a certain level until this volume of solution is displaced. The hydrometer is so designed that a portion of its graduated stem will stick out of the liquid surface. The surface of the liquid will be level with a Brix graduation mark.

The same will happen when the hydrometer is placed in solution B. But in this case, the volume of solution equal to the hydrometer’s weight W will be less, because the solution is denser. The hydrometer will, therefore, displace a smaller volume of solution—it will sink less than it did in solution A. The graduated stem will protrude more out of the liquid surface, at a higher Brix graduation mark. Figure 1.2 illustrates the experiment.

So, in fact, all that the immersed Brix hydrometer is doing is responding, according to the simple law of buoyancy, to the density of the solution. It is the calibrated graduated stem of the hydrometer that is interpreting this density into a Brix value, i.e., the amount of dissolved sugar in the solution. Solution A will have a lower Brix reading than solution B. This Brix/ density relationship is not as simple as it would appear from the above demonstration. Temperature now comes along and throws a spanner in the works.

Elementary physics teaches us that liquids expand with an increase of temperature and contract when cooled. This applies to sugar solutions as well. So, let us take for example the 1 liter of solution S (mentioned previously, with a weight of 1.034 kg and Brix of 9.20°B) and place it in the refrigerator for a while. It would cool and contract somewhat—it will no longer occupy a 1 liter volume but less than that. Let us say that the new cooled volume is now 998 ml (0.998 liter). The density would be calculated as follows:

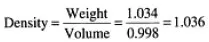
The density of solution S is now 1.036 and not 1.034 as it was before the solution was cooled in the refrigerator. This difference in densities, only in the third decimal place, may seem insignificant, but this is not the case. If the cooled solution had been measured with a Brix hydrometer, the new higher density would reflect an increase in Brix by about 0.6°B. This represents an apparent increase of about 6.5% sugar in the solution. There is, of course, no increase in sugar in the solution. What happened is that the change in temperature increased the solution’s density and would “fool” the Brix hydrometer if it were used to measure the sugar content.

20ºC is the standard temperature at which Brix values are determined.

Professor Brix was no fool. All Brix determinations are based on a standard temperature of 20°C. The Brix hydrometer has a built-in thermometer that records the temperature of the solution. This thermometer also has a graduated scale of precalculated standard temperature correction units. When the temperature is below 20°C, a correction is indicated as a subtraction from the Brix hydrometer reading. When above 20°C, a correction is added. In the above example, the Brix hydrometer would indicate a subtraction of 0.6°B from the actual reading—resulting in the original 9.20°B value.

FIGURE 1.2 The Brix/density relationship.

As I said previously, the Brix hydrometer is not used much any more—new sophisticated instruments and techniques are employed to determine Brix in the soft drinks industry. The hydrometer was discussed here mainly to demonstrate the relationship between density and Brix, which is still applicable in the new instruments.

DENSITY VS. SPECIFIC GRAVITY

Density and specific gravity are two ferent creatures altogether.

Density is often confused with specific gravity (SG), and as such, these two terms are sometimes incorrectly used. For liquids, SG can be defined as the ratio of the weight of a volume of the liquid to the weight of an equal volume of water at 4°C or other specified temperature.

The “weight of a volume” of a liquid is the liquid’s density. Therefore, SG is a ratio that merely compares the density of the liquid to the density of water and tells us how much lighter or heavier the liquid is than water. It does not give us an absolute weight of the liquid. Water at 4°C is at its highest density. At this temperature, 1 liter of water weighs 1 kg. Its density is, therefore, 1.000.

When referring to the SG of a liquid, the temperature of this liquid and that of the water need to be stated. This is normally accomplished by placing a two-temperature annotation following the SG term, such as “SG 4°C/4°C.” The first temperature is that of the liquid, the SG of which is being calculated. The second is that of the equal volume of water. This annotation is sometimes presented as:

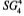
It is well known that water has a SG=1.000. This is because, by definition, this SG is calculated as follows:

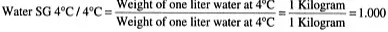
You may ask why I needed to show this calculation—one does not need to be a math genius to know that any number divided by itself will result in the value 1.000 (excluding zero, of course). The reason it is shown is that “later on” I wish to make a point using this same calculation format.

This SG of 1.000 often leads people in the industry to use this figure as the “universal” density of water. They therefore assume that 1 liter of water weighs 1 kg. This is incorrect—it is only true for water at 4°C.

The density of water at 20°C is 0.99717 kg/liter.

In our industry, we mostly deal with product water that is at ambient temperature. It is closer to 20°C, the standard temperature at which Brix is determined, than it is to 4°C. At 20°C, 1 liter of water will weigh less than 1 kg, because it is less dense than at 4°C—it will weigh 0.99717 kg. Therefore, it is erro neous to assume that water has a density of 1.000 as many people do—the correct factor to use for water volumes to weight conversion calculations is 0.99717. This is the first point in the confusion of density and SG that I want to highlight.

Density is the factor to be used in weight/volume conversion calculations—not SG.

The second area of confusion between SG and density occurs with sugar solution calculations. These calculations involve, among others, the need to convert beverage, fruit juice, and syrup volumes to weights, from milliliters to grams or from liters to kilograms and the reverse, to convert weights to volumes.

Standard Brix tables are available in which Brix values are given corresponding values of density at 20°C and SG values at 20°C/20°C. We often use these tables to find the factors of sugar solutions at different Brix values in order to calculate volume/weight conversions.

In such tables, at 9.2°B as an example:

The density column has a value of 1.03379

The SG column has a value of 1.03672

Which of these figures must we use to convert a liter of the 9.2°B solution to its weight in kilograms? In much the same way as was mentioned above for water, many people opt for the value in the SG column of the table. This again is an error. We must use the density value and not the SG figure. This is because the SG figure is based, by definition, on the ratio of the solution’s density at 20°C to the density of water at 20°C.

I will demonstrate this with the previous SG calculation format used for the SG calculation for water:

...

Table of contents

• COVER PAGE
• TITLE PAGE
• COPYRIGHT PAGE
• PREFACE
• INTRODUCTION TO SOFT DRINKS
• 1. BRIX—THE BASICS
• 2. TASTE TESTING—THEORY AND PRACTICE
• 3. FOOD LAWS—GENERAL ISSUES
• 4. EMULSIONS—THE CLOUDY DRINKS
• 5. WATER TREATMENT—THE KEY PROCESS
• 6. BRIX—SUGAR INVERSION
• 7. FRUIT JUICES—A SPECIAL TECHNOLOGY
• 8. FOOD LAWS—LABELING THE PACKAGE
• 9. SYRUP MAKING—THE HEART OF THE PROCESS
• 10. MICROBIOLOGY—ALL ABOUT THE “BUGS”
• 11. SYRUP SHRINKAGE—SPLITTING HAIRS?
• 12. CARBONATION—PUTTING IN THE FIZZ
• 13. UNITIZATION—A UNIQUE INGREDIENTS SYSTEM
• 14. FLAVORS—THE MAGICAL INGREDIENTS
• 15. FORMULATION—A SPREADSHEET TEMPLATE
• 16. MICROBIOLOGY—THE BIOFILM CONCEPT
• 17. QUALITY—THE KEY TO PERFORMANCE
• APPENDIX 1: BRIX/DENSITY CONVERSION TABLES
• APPENDIX 2: TEMPERATURE CORRECTION TABLES FOR REFRACTOMETRIC BRIX READINGS
• APPENDIX 3: SIGNIFICANCE TABLES FOR TWO-SAMPLE PREFERENCE TASTE TEST
• APPENDIX 4: SIGNIFICANCE TABLES FOR TRIANGULAR TASTE TEST
• APPENDIX 5: ACIDITY CORRECTION TABLES FOR REFRACTOMETRIC BRIX READINGS
• APPENDIX 6: MICROSOFT® EXCEL TEMPLATE FORZ FINAL BEVERAGE BRIX CALCULATION
• APPENDIX 7: GLOSSARY OF TECHNICAL AND GENERAL TERMS USED IN THIS HANDBOOK