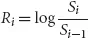Equity Derivatives and Hybrids
Markets, Models and Methods
Oliver Brockhaus
- English
- ePUB (handyfreundlich)
- Über iOS und Android verfügbar
Equity Derivatives and Hybrids
Markets, Models and Methods
Oliver Brockhaus
Über dieses Buch
Since the development of the Black-Scholes model, research on equity derivatives has evolved rapidly to the point where it is now difficult to cut through the myriad of literature to find relevant material. Written by a quant with many years of experience in the field this book provides an up-to-date account of equity and equity-hybrid (equity-rates, equity-credit, equity-foreign exchange) derivatives modeling from a practitioner's perspective. The content reflects the requirements of practitioners in financial institutions: Quants will find a survey of state-of-the-art models and guidance on how to efficiently implement them with regards to market data representation, calibration, and sensitivity computation. Traders and structurers will learn about structured products, selection of the most appropriate models, as well as efficient hedging methods while risk managers will better understand market, credit, and model risk and find valuable information on advanced correlation concepts.Equity Derivatives and Hybrids provides exhaustive coverage of both market standard and new approaches, including: -Empirical properties of stock returns including autocorrelation and jumps-Dividend discount models-Non-Markovian and discrete-time volatility processes-Correlation skew modeling via copula as well as local and stochastic correlation factors-Hybrid modeling covering local and stochastic processes for interest rate, hazard rate, and volatility as well as closed form solutions -Credit, debt, and funding valuation adjustment (CVA, DVA, FVA)-Monte Carlo techniques for sensitivities including algorithmic differentiation, path recycling, as well as multilevel.Written in a highly accessible manner with examples, applications, research, and ideas throughout, this book provides a valuable resource for quantitative-minded practitioners and researchers.
Häufig gestellte Fragen
Information
1 | 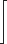 | Empirical Evidence |