
- 324 pages
- English
- ePUB (mobile friendly)
- Available on iOS & Android
Galois' Theory of Algebraic Equations
About this book
The book gives a detailed account of the development of the theory of algebraic equations, from its origins in ancient times to its completion by Galois in the nineteenth century. The appropriate parts of works by Cardano, Lagrange, Vandermonde, Gauss, Abel, and Galois are reviewed and placed in their historical perspective, with the aim of conveying to the reader a sense of the way in which the theory of algebraic equations has evolved and has led to such basic mathematical notions as "group" and "field".
A brief discussion of the fundamental theorems of modern Galois theory and complete proofs of the quoted results are provided, and the material is organized in such a way that the more technical details can be skipped by readers who are interested primarily in a broad survey of the theory.
In this second edition, the exposition has been improved throughout and the chapter on Galois has been entirely rewritten to better reflect Galois' highly innovative contributions. The text now follows more closely Galois' memoir, resorting as sparsely as possible to anachronistic modern notions such as field extensions. The emerging picture is a surprisingly elementary approach to the solvability of equations by radicals, and yet is unexpectedly close to some of the most recent methods of Galois theory.
Request Inspection Copy
The book gives a detailed account of the development of the theory of algebraic equations, from its origins in ancient times to its completion by Galois in the nineteenth century. The appropriate parts of works by Cardano, Lagrange, Vandermonde, Gauss, Abel, and Galois are reviewed and placed in their historical perspective, with the aim of conveying to the reader a sense of the way in which the theory of algebraic equations has evolved and has led to such basic mathematical notions as "group" and "field".
A brief discussion of the fundamental theorems of modern Galois theory and complete proofs of the quoted results are provided, and the material is organized in such a way that the more technical details can be skipped by readers who are interested primarily in a broad survey of the theory.
In this second edition, the exposition has been improved throughout and the chapter on Galois has been entirely rewritten to better reflect Galois' highly innovative contributions. The text now follows more closely Galois' memoir, resorting as sparsely as possible to anachronistic modern notions such as field extensions. The emerging picture is a surprisingly elementary approach to the solvability of equations by radicals, and yet is unexpectedly close to some of the most recent methods of Galois theory.
Request Inspection Copy
Readership: Upper level undergraduates, graduate students and mathematicians in algebra.
Key Features:
- Describes the problems and methods at the origin of modern abstract algebra
- Provides an elementary thorough discussion of the insolvability of general equations of degree at least five and of ruler-and-compass constructions
- Original exposition relying on early sources to set classical Galois theory into its historical perspective
Frequently asked questions
- Essential is ideal for learners and professionals who enjoy exploring a wide range of subjects. Access the Essential Library with 800,000+ trusted titles and best-sellers across business, personal growth, and the humanities. Includes unlimited reading time and Standard Read Aloud voice.
- Complete: Perfect for advanced learners and researchers needing full, unrestricted access. Unlock 1.4M+ books across hundreds of subjects, including academic and specialized titles. The Complete Plan also includes advanced features like Premium Read Aloud and Research Assistant.
Please note we cannot support devices running on iOS 13 and Android 7 or earlier. Learn more about using the app.
Information
Chapter 1
Quadratic Equations
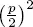
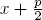
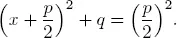
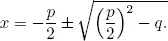
1.1Babylonian algebra
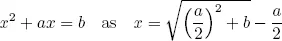
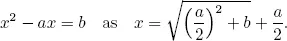



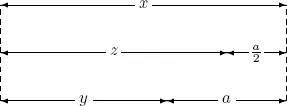
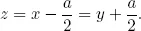
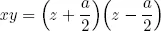
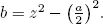
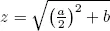
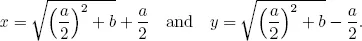

Table of contents
- Cover Page
- Title
- Copyright
- Dedication
- Preface to the Second Edition
- Preface to the First Edition (2001)
- Contents
- 1. Quadratic Equations
- 2. Cubic Equations
- 3. Quartic Equations
- 4. The Creation of Polynomials
- 5. A Modern Approach to Polynomials
- 6. Alternative Methods for Cubic and Quartic Equations
- 7. Roots of Unity
- 8. Symmetric Functions
- 9. The Fundamental Theorem of Algebra
- 10. Lagrange
- 11. Vandermonde
- 12. Gauss on Cyclotomic Equations
- 13. Ruffini and Abel on General Equations
- 14. Galois
- 15. Epilogue
- Selected Solutions
- Bibliography
- Index