Analytic Number Theory for Undergraduates

Heng Huat Chan

• Verlag: WSPC
• Jahr: 2009
• ISBN:
  9789814365277
• Thema: Mathematik
• Thema: Zahlentheorie

This book is written for undergraduates who wish to learn some basic results in analytic number theory. It covers topics such as Bertrand's Postulate, the Prime Number Theorem and Dirichlet's Theorem of primes in arithmetic progression.

The materials in this book are based on A Hildebrand's 1991 lectures delivered at the University of Illinois at Urbana-Champaign and the author's course conducted at the National University of Singapore from 2001 to 2008.

Contents:

• Facts about Integers
• Arithmetical Functions
• Averages of Arithmetical Functions
• Elementary Results on the Distribution of Primes
• The Prime Number Theorem
• Dirichlet Series
• Primes in Arithmetic Progression

Readership: Final-year undergraduates and first-year graduates with basic knowledge of complex analysis and abstract algebra; academics.

Chapter 1

The Fundamental Theorem of Arithmetic

1.1 Least Integer Axiom and Mathematical Induction

Let

Z = {0, ±1,±2,…}

be the set of integers. The Least Integer Axiom (see [10]), also known as the Well Ordering Principle, states that there is a smallest integer in every nonempty subset of non-negative integers. It is useful in establishing the following result.

Theorem 1.1. Let S (1), S(2),…, S(n),…be statements, one for each integer n ≥ 1. If some of these statements are false, then there is a first false statement.

Proof. Set

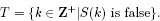
Since at least one statement is false, T is nonempty. By the Least Integer Axiom, there exists a smallest integer n in T. This implies that S(n) is the first false statement.

From Theorem 1.1, we deduce the Principle of Mathematical Induction.

Theorem 1.2. Let S(n) be statements, one for each n ≥ 1. Suppose that the following conditions are satisfied by S(n):

(a) The statement S(1) is true.

(b) If S(n) is true, then S(n + 1) is true.

Then S(n) is true for all integers n ≥ 1.

Proof. Suppose that S(n) is not true for all integers n ≥ 1. Then for some positive integer k ≥ 1, S(k) is false. By Theorem 1.1, there is a first false statement, say S(m). By the fact that S(1) is true, we conclude that m ≠ 1. Furthermore, by the minimality of m, we observe that S(j) is true for 1 < j ≤ m – 1. Now, by (b), S(m – 1) is true implies that S(m) is true. This contradicts the assumption that S(m) is false and we conclude that the statements S(n) is true for all positive integers n ≥ 1.

We may replace 1 in Theorem 1.2 (a) by any integer m. In other words, we can modify Theorem 1.2 as

Theorem 1.3. Let m be an integer. Let S(n) be statements, one for each integer n ≥ m. Suppose that the following two conditions are satisfied:

(a) The statement S(m) is true.

(b) If S(n) is true, then S(n + 1) is true.

Then S(n) is true for all integers n ≥ m.

We end this section with another version of the Principle of Mathematical Induction. The proof of this version is similar to the proof of Theorem 1.2 and we leave it as an exercise for the readers.

Theorem 1.4. Let m be an integer. Let S(n) be statements, one for each integer n ≥ m. Suppose that the following conditions are satisfied:

(a) S(m) is true and

(b) if S(k) is true for all m ≤ k ≤ n then S(n + 1) is true.

Then S(n) is true for all integers n ≥ m.

1.2 Division Algorithm

Theorem 1.5 (Division Algorithm). Let a and b be integers such that b > 0. Then there exist unique integers q and r with

a = bq + r, where 0 ≤ r < b.

Proof. Let

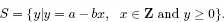
Note that since

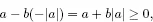
w...