Mathematics
Vector Product
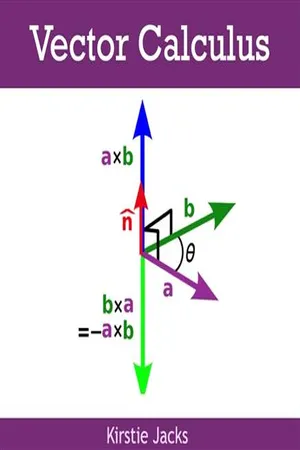
The vector product, also known as the cross product, is a mathematical operation that takes two vectors and produces a third vector perpendicular to the plane containing the original vectors. It is used in various mathematical and physical applications, such as calculating torque, angular momentum, and electromagnetic fields. The result of the cross product is a vector rather than a scalar.
Written by Perlego with AI-assistance
Related key terms
1 of 5
11 Key excerpts on "Vector Product"
- No longer available |Learn more
- (Author)
- 2014(Publication Date)
- Library Press(Publisher)
________________________ WORLD TECHNOLOGIES ________________________ Chapter 7 Cross Product In mathematics, the cross product , Vector Product or Gibbs Vector Product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them. It has many applications in mathematics, engineering and physics. If either of the vectors being multiplied is zero or the vectors are parallel then their cross product is zero. More generally, the magnitude of the product equals the area of a parallelogram with the vectors for sides; in particular for perpendicular vectors this is a rectangle and the magnitude of the product is the product of their lengths. The cross product is anticommutative, distributive over addition and satisfies the Jacobi identity. The space and product form an algebra over a field, which is neither commutative nor associative, but is a Lie algebra with the cross product being the Lie bracket. Like the dot product, it depends on the metric of Euclidean space, but unlike the dot product, it also depends on the choice of orientation or handedness. The product can be generalized in various ways; it can be made independent of orientation by changing the result to pseudovector, or in arbitrary dimensions the exterior product of vectors can be used with a bivector or two-form result. But if the product is limited to non-trivial products with vector results it only exists in three and seven dimensions. ________________________ WORLD TECHNOLOGIES ________________________ The cross-product in respect to a right-handed coordinate system ________________________ WORLD TECHNOLOGIES ________________________ Definition Finding the direction of the cross product by the right-hand rule The cross product of two vectors a and b is denoted by a × b . - No longer available |Learn more
- (Author)
- 2014(Publication Date)
- White Word Publications(Publisher)
________________________ WORLD TECHNOLOGIES ________________________ Chapter 5 Cross Product In mathematics, the cross product , Vector Product , or Gibbs Vector Product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them. It has many applications in mathematics, engineering and physics. If either of the vectors being multiplied is zero or the vectors are parallel then their cross product is zero. More generally, the magnitude of the product equals the area of a parallelogram with the vectors for sides; in particular for perpendicular vectors this is a rectangle and the magnitude of the product is the product of their lengths. The cross product is anticommutative, distributive over addition and satisfies the Jacobi identity. The space and product form an algebra over a field, which is neither commutative nor associative, but is a Lie algebra with the cross product being the Lie bracket. Like the dot product, it depends on the metric of Euclidean space, but unlike the dot product, it also depends on the choice of orientation or handedness. The product can be generalized in various ways; it can be made independent of orientation by changing the result to pseudovector, or in arbitrary dimensions the exterior product of vectors can be used with a bivector or two-form result. Also, using the orientation and metric structure just as for the traditional 3d cross product, one can in n dimensions take the product of n - 1 vectors to produce a vector perpendicular to all of them. But if the product is limited to non-trivial binary products with vector results it exists only in three and seven dimensions. ________________________ WORLD TECHNOLOGIES ________________________ The cross-product in respect to a right-handed coordinate system - James M. Van Verth, Lars M. Bishop(Authors)
- 2015(Publication Date)
- A K Peters/CRC Press(Publisher)
See Section 2.2.9 for more details. 2.2.8 Cross Product Suppose we have two vectors v and w and want to find a new vector u orthogonal to both. The operation that computes this is the cross product , also known as the Vector Product . There are two possible choices for the direction of the vector, each the negation of the other ( Figure 2.13 ); the one chosen is determined by the right-hand rule. Hold your right hand so that your forefinger points forward, your middle finger points out to the left, and your thumb points up. If you roughly align your forefinger with v , and your middle finger with w , then the cross product will point in the direction of your thumb ( Figure 2.14 ). The length of the cross product is equal to the area of a parallelogram bordered by the two vectors ( Figure 2.15 ). This can be computed using the formula v × w = v w sin θ (2.6) 52 Vectors and Points w v Figure 2.13. Two directions of orthogonal 3D vectors. w v v × w Figure 2.14. Cross product direction. w v v × w Figure 2.15. Cross product length equals area of parallelogram. 2.2 Vectors 53 where θ is the angle between v and w . Note that the cross product is not commutative, so order is important: v × w = − ( w × v ) Also, if the two vectors are parallel, sin θ = 0, so we end up with the zero vector. It is a common mistake to believe that if v and w are unit vectors, the cross product will also be a unit vector. A quick look at Equation 2.6 shows this is true only if sin θ is 1, in which case θ is 90 degrees. The formula for the cross product is v × w = ( v y w z − w y v z , v z w x − w z v x , v x w y − w x v y ) Certain processors can implement this as a two-step operation, by creating two vectors and performing the subtraction in parallel: v × w = ( v y w z , v z w x , v x w y ) − ( w y v z , w z v x , w x v y ) For vectors u , v , w , and scalar a , the following algebraic rules apply: 1. v × w = − w × v . 2. u × ( v + w ) = ( u × v ) + ( u × w ).- eBook - ePub
- Alan Durrant(Author)
- 2019(Publication Date)
- CRC Press(Publisher)
2.25 )) similar to those used in ordinary number algebra. Recall also that we cannot divide by a vector.Summary of section 2.4- The vector product , also called the cross product , is defined by(2.19)a × b =(| a || b | sinα ) n( 0 ≤ α ≤ 180 ° )where the direction of unit vector n is specified by the right-hand rule or the screw rule (Fig 2.13 ).
- The magnitude of the Vector Product a × b is the area of the parallelogram defined by displacements a and b (Fig 2.10a ).
- The collinearity condition for non-zero vectors is a × b = 0. An example is a × a = 0.
- Vector Products can be manipulated algebraically according to rules that are similar to those of ordinary number algebra except that the Vector Product is non-commutative (Eq (2.23 )) and there is no division by a vector.
Example 4.1 (Objective 7 ) Let u be of magnitude 5 directed towards the north and v of magnitude 3 directed 20° west of north (Fig 2.15 ). Specify the vectors u × v , v × u , u × u , u × (v + u ), –2u × 7v .Solution 4.1 The magnitudes are found from Eq (2.20 ) and the directions are specified by the right-hand rule or the screw rule. The magnitude |u × v | = 5×3 sin 20° = 5.13, and the direction of u × v is vertically upwards, i.e. in the direction of unit vector n pointing out of the plane of Fig 2.15 towards you. Thus u × v = 5.13n .v × u = –u × v = –5.13n .u × u = 0 (Eq (2.22 )).We can write u × (v + u ) = u × v + u × u = u × v since u × u = 0. u × v has already been specified as 5.13n .Finally, –2u × 7v = –14u × v = –71.8n .Example 4.2 (Objective 7 ) Consider the mutually orthogonal unit vectorsen,eeandeddirected towards the north, towards the east and vertically downwards respectively. Determine all possible Vector Products e i × e j where i and j can each be n, e or d - eBook - PDF
- James Stewart, Daniel K. Clegg, Saleem Watson, , James Stewart, James Stewart, Daniel K. Clegg, Saleem Watson(Authors)
- 2020(Publication Date)
- Cengage Learning EMEA(Publisher)
Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it. SECTION 12.4 The Cross Product 893 The Cross Product Given two nonzero vectors, it is very useful to be able to find a nonzero vector that is perpendicular to both of them, as we will see in the next section and in Chapters 13 and 14. We now define an operation, called the cross product, that produces such a vector. ■ The Cross Product of Two Vectors Given two nonzero vectors a - k a 1 , a 2 , a 3 l and b - k b 1 , b 2 , b 3 l, suppose that a nonzero vector c - k c 1 , c 2 , c 3 l is perpendicular to both a and b. Then a c - 0 and b c - 0 and so 1 a 1 c 1 1 a 2 c 2 1 a 3 c 3 - 0 2 b 1 c 1 1 b 2 c 2 1 b 3 c 3 - 0 To eliminate c 3 we multiply (1) by b 3 and (2) by a 3 and subtract: 3 sa 1 b 3 2 a 3 b 1 d c 1 1 sa 2 b 3 2 a 3 b 2 d c 2 - 0 Equation 3 has the form pc 1 1 qc 2 - 0, for which an obvious solution is c 1 - q and c 2 - 2p. So a solution of (3) is c 1 - a 2 b 3 2 a 3 b 2 c 2 - a 3 b 1 2 a 1 b 3 Substituting these values into (1) and (2), we then get c 3 - a 1 b 2 2 a 2 b 1 This means that a vector perpendicular to both a and b is k c 1 , c 2 , c 3 l - k a 2 b 3 2 a 3 b 2 , a 3 b 1 2 a 1 b 3 , a 1 b 2 2 a 2 b 1 l The resulting vector is called the cross product of a and b and is denoted by a 3 b. 4 Definition of the Cross Product If a - k a 1 , a 2 , a 3 l and b - k b 1 , b 2 , b 3 l, then the cross product of a and b is the vector a 3 b - k a 2 b 3 2 a 3 b 2 , a 3 b 1 2 a 1 b 3 , a 1 b 2 2 a 2 b 1 l Hamilton The cross product was invented by the Irish mathematician Sir William Rowan Hamilton (1805–1865), who had created a precursor of vectors, called quaternions. - Adrian Burd(Author)
- 2019(Publication Date)
- Cambridge University Press(Publisher)
The converse of this is that three vectors are linearly independent if their scalar triple product is nonzero. Exercise 4.3.13 Show that if u is a linear combination of v and w, then u · (v × w) = 0. Exercise 4.3.14 Show that the vectors u = ˆ ı + ˆ j − ˆ k, v = 2ˆ ı − ˆ j + 3 ˆ k, and w = 3ˆ ı + 2 ˆ k are coplanar. The last Vector Product we will talk about is the vector triple product. This is something of a complicated beast. If we have three vectors A, B, and C, then the vector triple product is A × (B × C). The vector U = B × C is a vector that is perpendicular to both B and C. So, the vector A × (B × C) = A × U is a vector that is perpendicular to both A and B × C, and so must lie in the same plane as B and C (Figure 4.16). The vector triple product can be expressed as the difference of two vectors, A × (B × C) = (A · C)B − (A · B)C. (4.45) Equation (4.45) may look a little strange at first, but recall that the scalar product of two vectors is just a number, so the vector triple product A × (B × C) is a linear combination of the vectors B and C, which we can also see from Figure 4.16. As we can see from Equation (4.45), the placement of the parentheses is very important. In fact, because the vector cross 187 4.4 Matrices n A A p Figure 4.17 The projection of the vector A into a plane that has a unit normal n is A p . product does not commute (i.e., A × B = −B × A), we can see that, for example, A × (B × C) = −(B × C) × A. We can use the vector triple product to calculate the projection (A p ) of a vector A into a plane that has a unit normal vector n (Figure 4.17). The simplest way to calculate A p is to realize that the component of A perpendicular to the plane is just A · n, and then A p = A − (A · n)n. But we can also use the vector triple product, because using Equation (4.45) we find n × (A × n) = (n · n)A − (A · n)n = A − (A · n)n, which is the same formula we had before.- eBook - PDF
- Morton E. Gurtin, Eliot Fried, Lallit Anand(Authors)
- 2010(Publication Date)
- Cambridge University Press(Publisher)
The term point will be reserved for elements of E and the term vector for elements of the associated vector space V . Then: (i) The difference v = y − x between the points y and x is a vector. (ii) The sum y = x + v of a point x and a vector v is a point. (iii) Unlike the sum of two vectors, the sum of two points has no meaning. 1.1 Inner Product. Cross Product Our assumption that the point space E be Euclidean automatically endows the asso-ciated vector space V with an inner product. 3 We use the standard notation of vector analysis. In particular, • The inner product (a scalar) and cross product (a vector) 4 of vectors u and v are respectively designated by u · v and u × v . 3 The inner product is often referred to as the dot product. 4 We assume that the reader has some familiarity with these notions. The cross product is ordered in the sense that the cross product u × v of u and v is not generally equal to the cross product v × u of v and u . 3 4 Vector Algebra Figure 1.1. The parallelogram P defined by the vectors u and v and the direction of u × v determined by the right-hand screw rule. The inner product determines the magnitude (or length) of a vector u via the relation | u | = √ u · u ; and the angle θ = ∠ ( u , v ) (1.1) between nonzero vectors u and v is defined by cos θ = u · v | u || v | (0 ≤ θ ≤ π ) . (1.2) Since −| u || v | ≤ u · v ≤ | u || v | , this definition assigns exactly one angle θ to each pair of nonzero vectors u and v . Trivially, u · v = | u || v | cos θ ; this relation is often used to define the inner product. With regard to the cross product, the magnitude | u × v | (1.3) represents the area spanned by the vectors u and v ; that is, the area of the parallelogram P defined by these vectors as indicated in Figure 1.1 ; this area is nonzero if and only if u and v are linearly independent . - eBook - PDF
- Daniel A. Fleisch(Author)
- 2011(Publication Date)
- Cambridge University Press(Publisher)
2.4 Triple Vector Product 33 (since both operations are cross products). You should note that A × ( B × C ) is not the same as ( A × B ) × C ; the location of the parentheses matters greatly in the triple Vector Product. The triple Vector Product is somewhat tedious to calculate by brute force, but thankfully a simplified expression exists: A × ( B × C ) = B ( A ◦ C ) − C ( A ◦ B ). (2.14) After all the previous discussion of the various ways in which vectors can be multiplied, you can be forgiven for thinking that the right side of this equation looks a bit strange, with no circle or cross between B and A ◦ C or between C and A ◦ B . Just remember that A ◦ C and A ◦ B are scalars, so the expressions in parentheses in Eq. 2.14 are simply scalar multipliers of vectors B and C . Does this mean that the result of the operation A × ( B × C ) is a vector that is some linear combination of the second and third vectors in the triple product? That’s exactly what it means, as you can see by considering Figure 2.5 . In this figure, you can see the vector B × C pointing straight up, perpendic-ular to the plane containing vectors B and C . Now imagine forming the cross product of vector A with vector B × C by pushing A into the direction of B × C with the palm of your right hand. The result of this operation, labelled vector A × ( B × C ) , is back in the plane containing vectors B and C . To understand why this is true, consider the fact that the vector that results from the operation B × C must be perpendicular to the plane containing B and C . If you now cross A into that vector, the resulting vector must be perpendicular to both A and to ( B × C ), which puts it back in the plane containing vectors B and C . And if the vector result of the operation A × ( B × C ) is in the same plane as vectors B and C , then it must be a linear combination of those two vectors. - Adrian B. Biran(Author)
- 2010(Publication Date)
- CRC Press(Publisher)
Mind that the MATLAB command cross produces a vector, while the command det yields a number. A geometrical interpretation of the determinant of a 3-by-3 matrix is given in the next subsection. 2.4.2 The scalar triple product. Parallelepiped volume Three vectors, V 1 , V 2 , V 3 , can be multiplied in several ways. We are going to deal with one of these ways: first build the Vector Product V 2 × V 3 , next calculate the scalar product of V 1 by the Vector Product, that is w = V 1 · ( V 2 × V 3 ) (2.6) The scalar w is the scalar triple product , or mixed product of V 1 , V 2 , and V 3 . As shown in Subsection 2.4.1, the cross product yields a vector whose magnitude equals the area of the parallelogram defined by the vectors Vectors and matrices 81 V 2 , V 3 . Let us call this vector A , an abbreviation of ‘Area’. Let the angle between V 1 and A be β. The scalar product of V 1 and A is V 1 · A = V 1 · A sin β But V 1 · sin β is the height of the end of V 1 above the plane defined by the other two vectors. Multiplying this height by the area of the parallelogram we obtain the volume of the parallelepiped defined by the three vectors. This geometrical interpretation is illustrated in Figures 2.18 and 2.19. To give an example of calculation in MATLAB, let us reuse, but with a ‘shifted’ notation, the two vectors, V 1 , V 2 defined in Subsection 2.4.1, and define a third vector inclined 45 o with respect to the plane defined by the first two vectors (the xy − plane).- No longer available |Learn more
- James Stewart, Lothar Redlin, Saleem Watson(Authors)
- 2016(Publication Date)
- Cengage Learning EMEA(Publisher)
640 CHAPTER 9 ■ Vectors in Two and Three Dimensions DEFINITION OF THE DOT PRODUCT If u 8 a 1 , a 2 9 and v 8 b 1 , b 2 9 are vectors, then their dot product, denoted by u # v, is defined by u # v a 1 b 1 a 2 b 2 Thus to find the dot product of u and v, we multiply corresponding components and add. The dot product is not a vector; it is a real number, or scalar. EXAMPLE 1 ■ Calculating Dot Products (a) If u 3, 2 and v 4, 5 then u # v 1 3 21 4 2 1 2 21 5 2 2 (b) If u 2 i j and v 5 i 6 j, then u # v 1 2 21 5 2 1 1 21 6 2 4 Now Try Exercises 5(a) and 11(a) ■ The proofs of the following properties of the dot product follow easily from the definition. PROPERTIES OF THE DOT PRODUCT 1. u # v v # u 2. 1 c u 2 # v c 1 u # v 2 u # 1 c v 2 3. 1 u v 2 # w u # w v # w 4. 0 u 0 2 u # u Proof We prove only the last property. The proofs of the others are left as exercises. Let u 8 a 1 , a 2 9 . Then u # u a 1 a 1 a 2 a 2 a 2 1 a 2 2 0 u 0 2 ■ Let u and v be vectors, and sketch them with initial points at the origin. We define the angle u between u and v to be the smaller of the angles formed by these represen- tations of u and v (see Figure 1). Thus 0 u p. The next theorem relates the angle between two vectors to their dot product. THE DOT PRODUCT THEOREM If u is the angle between two nonzero vectors u and v, then u # v 0 u 00 v 0 cos u Proof Applying the Law of Cosines to triangle AOB in Figure 2 gives 0 u v 0 2 0 u 0 2 0 v 0 2 2 0 u 00 v 0 cos u y x 0 v u ¨ FIGURE 1 Copyright 2017 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. - eBook - PDF
Calculus
One and Several Variables
- Saturnino L. Salas, Garret J. Etgen, Einar Hille(Authors)
- 2011(Publication Date)
- Wiley(Publisher)
Think instead of using the operations we have defined on vectors: addition, subtraction, scalar multiplication, dot product, cross product. Being geometrically motivated, these operations are likely to provide greater understanding than breaking up everything in sight into components. ❏ Example 4 Verify Lagrange’s identity: a × b 2 + (a · b) 2 = a 2 b 2 . SOLUTION We could begin by writing a × b 2 = (a 2 b 3 − a 3 b 2 ) 2 + (a 1 b 3 − a 3 b 1 ) 2 + (a 1 b 2 − a 2 b 1 ) 2 (a · b) 2 = (a 1 b 1 + a 2 b 2 + a 3 b 3 ) 2 a 2 b 2 = (a 2 1 + a 2 2 + a 2 3 )(b 2 1 + b 2 2 + b 2 3 ), but this would take us into a morass of arithmetic. It is much more fruitful to proceed as follows: a × b = ab sin θ and a · b = ab cos θ. Therefore a × b 2 + (a · b) 2 = a 2 b 2 sin 2 θ + a 2 b 2 cos 2 θ = a 2 b 2 (sin 2 θ + cos 2 θ ) = a 2 b 2 . ❏ Remark Lagrange’s identity is one more dividend we get from the apparently arbi- trary definition of a × b. ❏ Three Additional Identities You have seen that the cross product is not commutative. It is also not associative: the vectors a × (b × c) and (a × b) × c are generally not the same. For example, i × (i × j) = i × k = −j but (i × i) × j = 0 × j = 0. What is true instead is that a × (b × c) = (a · c)b − (a · b)c, (13.4.11) (a × b) × c = (c · a)b − (c · b)a. 670 ■ CHAPTER 13 VECTORS IN THREE-DIMENSIONAL SPACE There is one more identity that we want to mention: (13.4.12) (a × b) · (c × d) = (a · c)(b · d) − (a · d)(b · c). The verification of these three identities is left to you in the Exercises. Remark Dot products and cross products appear frequently in physics and in en- gineering. Work is a dot product. So is the power expended by a force. Torque and angular momentum are cross products. Turn on a television set and watch the dots on the screen. How they move is determined by the laws of electromagnetism.
Index pages curate the most relevant extracts from our library of academic textbooks. They’ve been created using an in-house natural language model (NLM), each adding context and meaning to key research topics.