What is Game Theory?
MA, Management Science (University College London)
Date Published: 15.03.2023,
Last Updated: 19.07.2024
Share this article
Defining Game Theory
Our daily lives are made up of interactions with different people, agents and institutions. These interactions can range from cooperation to conflict. For instance, with friends, you will cooperatively exchange ideas to decide on the plans for the weekend based on everyone’s preferences. At the workplace, companies will look at what competitors are doing to decide what their next move in the market will be. The beauty of humanity is that we are all interrelated, and the decisions of one actor will influence and be influenced by the decisions of others. Game theory allows us to understand how people act in situations where they are interconnected. It does so by treating individuals as players in a game, assuming that every player is rational (i.e., makes decisions in pursuit of their own objectives) and intelligent. As described by the theorist and Nobel Prize winner Roger B. Myerson in his book Game Theory: Analysis of Conflict, game theory situations are best represented using mathematical models.
Game theory is the study of mathematical models of conflict and cooperation between intelligent rational decision-makers. (2013)
Roger B. Myerson
Game theory is the study of mathematical models of conflict and cooperation between intelligent rational decision-makers. (2013)
How was game theory born?
Most of the early developments of game theory happened at the University of Princeton in the early 1920’s. It was John Von Neumann, the renowned Hungarian-American mathematician, who first explored this science of strategy known as game theory. The culmination of his findings were condensed in the book Theory of Games and Economic Behaviour, which he published in 1944 and co-wrote with his fellow colleague and economist Oskar Morgenstern. In the book, they argued that any economic situation could be looked at as a game between two competing actors.
The next stage develops when the theory is to somewhat more complicated situations in which it may already lead to a certain extent beyond the obvious and the familiar. Here theory and application corroborate each other mutually. Beyond this lies the field of real success: genuine prediction by theory. It is well known that all mathematized sciences have gone through these successive phases of evolution. (2015)
John Von Neumann, Oskar Morgenstern
The next stage develops when the theory is to somewhat more complicated situations in which it may already lead to a certain extent beyond the obvious and the familiar. Here theory and application corroborate each other mutually. Beyond this lies the field of real success: genuine prediction by theory. It is well known that all mathematized sciences have gone through these successive phases of evolution. (2015)
Their conclusions rapidly drew the attention of economists and politicians of the time, who found extreme value and relevance in the applications of game theory to warfare matters during WWII and the beginning of the Cold War. More specifically, game theory soon became the theoretical foundation for war analysts and politicians to locate enemy submarines. A strategy was desperately needed to ensure torpedoes were fired where enemy warships were located. For that, it was necessary to act based on what the enemy was doing and game theory could provide the answers.
John Nash, a mathematics graduate at the University of Princeton soon became the next groundbreaking theorist to unlock a whole new outlook for game theory. In the early 1950’s he came up with a way of solving non-cooperative games (ie., where players act independently) such that all players win because everyone gets the outcome they desire. As explained in the book The Essential John Nash, this outcome of mutual player contentment is known as the Nash equilibrium. It is the combination or set of player moves such that no player finds any additional benefit in choosing a different strategy; all players are satisfied with their game choices at the same time, so the game remains at equilibrium.
Nash equilibrium - a configuration of strategies, such that no player acting on his own can change his strategy to achieve a better outcome for himself.
The Nash equilibrium marked a turning point for game theory. John Nash had found a simple and highly applicable way of solving problems in all kinds of contexts. His disruptive discovery gained respect and notoriety, resulting in best-selling books (and later film adaptation) “A Beautiful Mind”.
But the bizarre and elaborate character of Nash’s beliefs, which were simultaneously grandiose and persecutory, his tense, suspicious, guarded behaviour, the relative coherence of his speech, the blankness of his facial expressions, and the extreme detachment of his voice, the reserve which bordered at times on muteness — all pointed toward schizophrenia.
Even though Nash’s theory received a lot of praise and admiration, some “hated” his findings. Indeed, Von Neumann, the founding father of game theory, was against a single-point solution. Other theorists remained open-minded to Nash’s discoveries and decided to address the loopholes of game theory to the date, refining and improving the generalisability of Nash’s theory. In the 1960’s, economists Thomas Schelling, Reinhard Selten and John Harsanyi addressed issues in games with multiple Nash equilibria, or where players could not communicate or had incomplete information. In 1994, Nash, Shelling and Hirsanyi won the Nobel Prize for their pioneering analysis of game theory in non-cooperative games.
How does game theory work?
The Prisoner's Dilemma came about in the RAND Corporation (department of Research and Development of the US Air Force) in 1950. It is a game or strategic interaction which has been widely used to illustrate and exemplify the workings of game theory.
The book Game Theory: An Introduction by 50Minutes.com briefly explains the essence of this dilemma:
Two thieves are arrested by the police and interrogated separately. The police are convinced they are guilty, but do not yet have sufficient evidence to heavily sentence them. Between them, before the arrest, the thieves vowed not to betray one another. The police, who want more than anything to get the confessions of the two men, promise freedom to the person that speaks, if he is the only man to do so. Hence a dilemma arises: on the one hand, the prisoners know that they will only suffer a small penalty if they do not confess to the police. On the other hand, both are individually tempted to confess the crime to gain freedom. (2016)
50MINUTES.COM
Two thieves are arrested by the police and interrogated separately. The police are convinced they are guilty, but do not yet have sufficient evidence to heavily sentence them. Between them, before the arrest, the thieves vowed not to betray one another. The police, who want more than anything to get the confessions of the two men, promise freedom to the person that speaks, if he is the only man to do so. Hence a dilemma arises: on the one hand, the prisoners know that they will only suffer a small penalty if they do not confess to the police. On the other hand, both are individually tempted to confess the crime to gain freedom. (2016)
The two players can choose between two strategies: “deny” or “confess”. Depending on what they choose, they will spend more or less years in prison. In the matrix, the payoffs (i.e, the years that they spend in prison) are the numbers in each of the boxes. The first digit corresponds to the years spent in prison by Player 1 and the second, those spent in prison by Player 2. For example, if Player 1 confesses and Player 2 denies, they will spend 0 and 5 years in prison respectively.
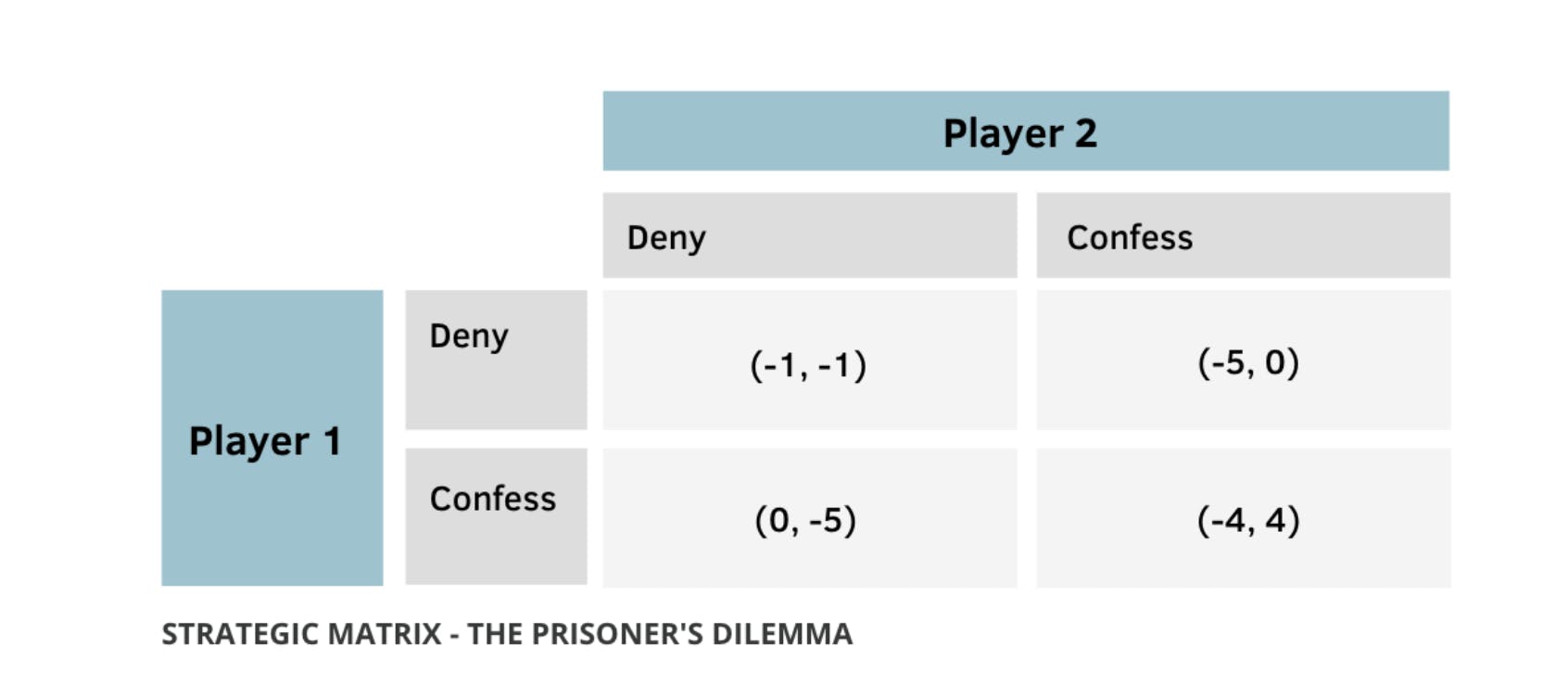
The objective of both players is to minimise the time spent in prison. To find the Nash equilibrium, you ask yourself “If Player 1 denies, what is the best thing Player 2 can do?”. In this case, Player 2 is better off confessing since he would spend 0 years in prison given that Player 1 denied. Following this procedure for all possible actions and for both players will yield the Nash equilibrium, the strategy where no player will want to dive. To see the full working out of the procedure, you can follow this link to a one page infographic. In this case, the Nash equilibrium occurs when both Players confess.
What are some uses of Game Theory in real life?
Being in a situation similar to the prisoner’s dilemma is not uncommon. This becomes obvious in the book Introducing Game Theory, which illustrates game theory’s applications in a wide range of contexts.
In economics, the decisions of firms are affected by their expectations of a competitor’s choice of product, price and advertising. In political science, a candidate’s policy platform is influenced by the policy announcements of their rival. In biology, animals must compete for scarce resources, but can be hurt if they are too aggressive with the wrong rival. In computer science, networked computers compete for bandwidth. In sociology, public displays of non-conformist attitudes are influenced by others’ behaviour, which is shaped by social culture. (2017)
Ivan Pastine, Tuvana Pastine, Tom Humberstone
In economics, the decisions of firms are affected by their expectations of a competitor’s choice of product, price and advertising. In political science, a candidate’s policy platform is influenced by the policy announcements of their rival. In biology, animals must compete for scarce resources, but can be hurt if they are too aggressive with the wrong rival. In computer science, networked computers compete for bandwidth. In sociology, public displays of non-conformist attitudes are influenced by others’ behaviour, which is shaped by social culture. (2017)
Indeed, the applications of game theory are infinite ranging from economics, politics, biology, computer science or sociology to name a few. Most commonly, the strategy departments of businesses will use game theory to understand how to react to competitor actions. For example, say there are two main competing firms in an industry: Firm A and Firm B. Recently, Firm A has been reconsidering their pricing strategy, looking at whether they should increase or decrease their prices to boost their revenues. Firm B intends to use game theory to understand what their best response to Firm A’s pricing strategy will be. This example can be solved just like the prisoner's dilemma. Both companies can choose between two strategies: increase or decrease their market price. Their payoffs are the revenue gains or losses generated from their chosen pricing strategy. Firm B will find the Nash equilibrium to decide what their optimal response strategy will be.
What are some limitations of game theory in real life?
Born in the 1920’s, game theory is a relatively young field of study which has received weighty academic attention for over a century. In a way, this discipline empowers individuals to predict the unpredictability of human behaviour. However, any science, mathematical or theoretical model will have its own limitations which will constrain its generalisability to all scenarios.
In the opening of the article, game theory is defined under the assumption that all humans are rational. That is, game theory assumes that individuals will make the choices that benefit them the most. However, as explained in the book Introducing Game Theory, people will not always have the desire of maximising their utility when making a decision. Think of NGOs or kidney donors; they will not always make the choice that is most rational or beneficial to themselves.
The concept of rationality requires unlimited cognitive capabilities. Fully rational man knows the solutions of all mathematical problems and can immediately perform all computations, regardless of how difficult they are.
Along with the unrealistic assumption of human rationality, the incompleteness of information in strategic scenarios has been another main criticism around game theory from its early beginnings. Indeed, game theory assumes that players know their payoffs under different strategies. In reality, outcomes are just as unpredictable as human behaviour itself.
These small details and assumptions may condition the accuracy of game theory. Therefore, it is important to be mindful of the fine line between hypothesising the outcome of strategic behaviours versus making blunt conclusions and statements on future human behaviour.
Closing thoughts
To conclude, the study of game theory is undoubtedly one of the most complex and ambitious fields of microeconomics. It is complex because there are a plethora of potential situations and strategic interactions that can happen in real life that game theory must find answers to. Attempting to put a mathematical framework around this complexity and the unpredictability of human behaviour makes game theory an ambitious and beautiful science.
Further game theory reading on Perlego
To read more about the applications of game theory to climate change, Game Theory and Climate Change by Parkash Chander
To read more about the applications of game theory to political science, Game Theory for Political Scientists by James D. Morrow
To read more about the applications of game theory to sports and soccer, Beautiful Game Theory by Ignacio Palacios Huerta
To read more about the applications of game theory in business management, Game Theory in Management by Michael Hatfield
Bibliography
Myerson, R. (2013) Game Theory. Harvard University Press. Available at: https://www.perlego.com/book/1147792/game-theory-analysis-of-conflict-pdf (Accessed: 14 February 2023).
Universalis, E. (2015) Theory of Games and Economic Behavior de Christian Morgenstern. Encyclopaedia Universalis. Available at: https://www.perlego.com/book/3571154/theory-of-games-and-economic-behavior-de-christian-morgenstern-les-fiches-de-lecture-duniversalis-pdf (Accessed: 14 February 2023).
Nash, J. (2016) The Essential John Nash. Princeton University Press. Available at: https://www.perlego.com/book/737869/the-essential-john-nash-pdf (Accessed: 14 February 2023).
Nasar, S. (2011) A Beautiful Mind. Simon & Schuster. Available at: https://www.perlego.com/book/779628/a-beautiful-mind-pdf (Accessed: 14 February 2023).
50MINUTES.com (2016) Game Theory. 50Minutes.com. Available at: https://www.perlego.com/book/9331/game-theory-the-art-of-thinking-strategically-pdf (Accessed: 14 February 2023).
Pastine, I., Pastine, T. and Humberstone, T. (2017) Introducing Game Theory. Icon Books. Available at: https://www.perlego.com/book/569883/introducing-game-theory-a-graphic-guide-pdf (Accessed: 14 February 2023).
MA, Management Science (University College London)
Inés Luque has a Masters degree in Management Science from University College London. During high school, she developed a strong interest in Economics, leading her to win the national Economics prize in her country of nationality, Spain. Her expertise is in the areas of microeconomics, game theory and design of incentives. Inés is passionate about the publishing industry and is currently working in the consulting department of the Financial Times in London.




